
科目: 来源: 题型:
【题目】据统计,某小区2011年底拥有私家车125辆,2013年底私家车的拥有量达到180辆.
(1)若该小区2011年底到2014年底私家车拥有量的年平均增长率相同,则该小区到2014年底私家车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1 000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
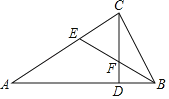
(1)求证:△AEB~△CFB;
(2)若AE=2EC,BC=6.求AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y1=x2+bx+c与直线y2=﹣2x+m相交于A(﹣2,n)、B(2,﹣3)两点.
(1)求这条抛物线的解析式;
(2)若点D为抛物线的顶点,求三角形ABD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+bx+c=0.
(1)若b=2m﹣1,m+c=﹣6,判断方程根的情况;
(2)若方程有两个相等的非零实数根,且b2﹣c2﹣4=0,求此时方程的根.
查看答案和解析>>
科目: 来源: 题型:
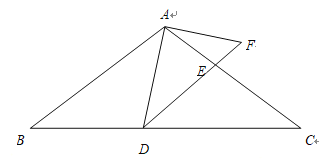
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
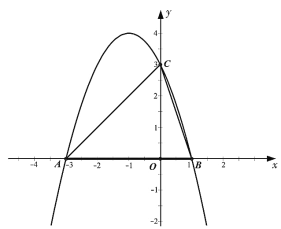
【题目】如图,抛物线与![]() 轴相交于点
轴相交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一动点, 联结
是抛物线上一动点, 联结![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求这条抛物线的解析式,并写出顶点坐标;
(2)求![]() 的正切值;
的正切值;
(3)当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,为放置在水平桌面![]() 上的台灯,底座的高
上的台灯,底座的高![]() 为
为![]() .长度均为
.长度均为![]() 的连杆
的连杆![]() ,
,![]() 与
与![]() 始终在同一水平面上.
始终在同一水平面上.
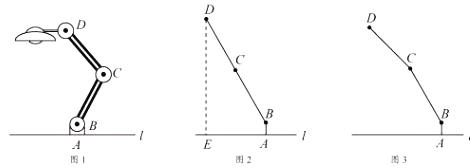
(1)旋转连杆![]() ,
,![]() ,使
,使![]() 成平角,
成平角,![]() ,如图2,求连杆端点
,如图2,求连杆端点![]() 离桌面
离桌面![]() 的高度
的高度![]() .
.
(2)将(1)中的连杆![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,如图3,问此时连杆端点
,如图3,问此时连杆端点![]() 离桌面
离桌面![]() 的高度是增加了还是减少?增加或减少了多少?(精确到
的高度是增加了还是减少?增加或减少了多少?(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
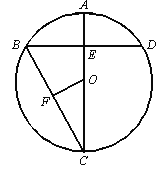
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com