
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B,与y轴分别交于点C,其中点
与x轴交于点A、B,与y轴分别交于点C,其中点![]() ,点
,点![]() ,且
,且![]() .
.
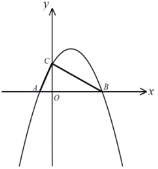
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,过P作![]() 交BC于D,当
交BC于D,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(3)点M是位于线段BC上方的抛物线上一点,当![]() 恰好等于
恰好等于![]() 中的某个角时,求点M的坐标.
中的某个角时,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,P是BC上一动点,过P作AP的垂线交CD于E,将
,P是BC上一动点,过P作AP的垂线交CD于E,将![]() 翻折得到
翻折得到![]() ,延长FP交AB于H,连结AE,PE交AC于G.
,延长FP交AB于H,连结AE,PE交AC于G.
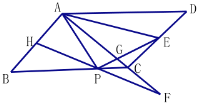
(1)求证![]() ;
;
(2)当![]() 时,求AE的长;
时,求AE的长;
(3)当![]() 时,求AG的长.
时,求AG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】成都市某景区经营一种新上市的纪念品,进价为20元/件,试营销阶段发现;当销售单价是30元时,每天的销售量为200件;销售单价每上涨2元,每天的销售量就减少10件.这种纪念品的销售单价为x(元).
(1)试确定日销售量y(台)与销售单价为x(元)之间的函数关系式;
(2)若要求每天的销售量不少于15件,且每件纪念品的利润至少为30元,则当销售单价定为多少时,该纪念品每天的销售利润最大,最大利润为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的盒子里装有5个分别写有数字0,1,2,3,4的小球,它们除数字不同外其余全部相同.现从盒子里随机摸出一个小球(不放回),设该小球上的数字为m,再从盒子中摸出一个小球,设该小球上的数字为n,点P的坐标为![]() ,则点P落在抛物线
,则点P落在抛物线![]() 与x轴所围成的区域内(含边界)的概率是________.
与x轴所围成的区域内(含边界)的概率是________.
查看答案和解析>>
科目: 来源: 题型:
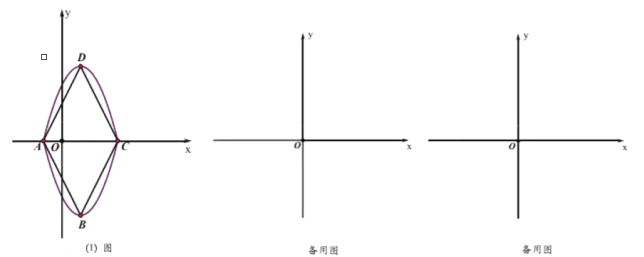
【题目】定义:在平面直角坐标系中,抛物线![]() (
(![]() )与直线
)与直线![]() 交于点
交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 右边),将抛物线
右边),将抛物线![]() 沿直线
沿直线![]() 翻折,翻折前后两抛物线的顶点分别为点
翻折,翻折前后两抛物线的顶点分别为点![]() 、
、![]() ,我们将两抛物线之间形成的封闭图形称为惊喜线,四边形
,我们将两抛物线之间形成的封闭图形称为惊喜线,四边形![]() 称为惊喜四边形,对角线
称为惊喜四边形,对角线![]() 与
与![]() 之比称为惊喜度(Degree of surprise),记作
之比称为惊喜度(Degree of surprise),记作![]() .
.
(1)如图(1)抛物线![]() 沿直线
沿直线![]() 翻折后得到惊喜线.则点
翻折后得到惊喜线.则点![]() 坐标 ,点
坐标 ,点![]() 坐标 ,惊喜四边形
坐标 ,惊喜四边形![]() 属于所学过的哪种特殊平行四边形? ,
属于所学过的哪种特殊平行四边形? ,![]() 为 .
为 .
(2)如果抛物线![]() (
(![]() )沿直线
)沿直线![]() 翻折后所得惊喜线的惊喜度为1,求
翻折后所得惊喜线的惊喜度为1,求![]() 的值.
的值.
(3)如果抛物线![]() 沿直线
沿直线![]() 翻折后所得的惊喜线在
翻折后所得的惊喜线在![]() 时,其最高点的纵坐标为16,求
时,其最高点的纵坐标为16,求![]() 的值并直接写出惊喜度
的值并直接写出惊喜度![]() .
.
查看答案和解析>>
科目: 来源: 题型:
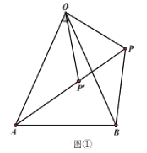
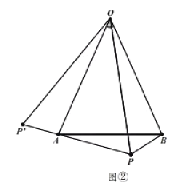
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 外一点,将
外一点,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,且点
,且点![]() 、
、![]() 、
、![]() 三点在同一直线上.
三点在同一直线上.
(1)(观察猜想)
在图①中,![]() ;在图②中,
;在图②中,![]() (用含
(用含![]() 的代数式表示)
的代数式表示)
(2)(类比探究)
如图③,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,探究线段
,探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)(问题解决)
若![]() ,
,![]() ,
,![]() ,求点
,求点![]() 到
到![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
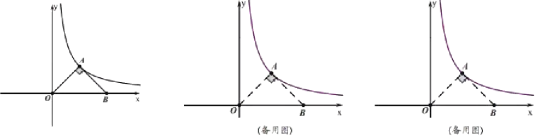
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为原点
为原点![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
(1)求反比例函数的解析式:
(2)将![]() 向右平移
向右平移![]() 个单位长度,对应得到
个单位长度,对应得到![]() ,当函数
,当函数![]() 的图象经过
的图象经过![]() 一边的中点时,求
一边的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月5日,第二届中国国际进口博览会(The 2nd China International lmport Expo)在上海国家会展中心开幕.本次进博会将共建开放合作、创新共享的世界经济,见证海纳百川的中国胸襟,诠释兼济天下的责任担当.小滕、小刘两人想到四个国家馆参观:![]() .中国馆;
.中国馆;![]() .俄罗斯馆;
.俄罗斯馆;![]() .法国馆;
.法国馆;![]() .沙特阿拉伯馆.他们各自在这四个国家馆中任意选择一个参观,每个国家馆被选择的可能性相同.
.沙特阿拉伯馆.他们各自在这四个国家馆中任意选择一个参观,每个国家馆被选择的可能性相同.
(1)求小滕选择![]() .中国馆的概率;
.中国馆的概率;
(2)用画树状图或列表的方法,求小滕和小刘恰好选择同一国家馆的概率.

查看答案和解析>>
科目: 来源: 题型:
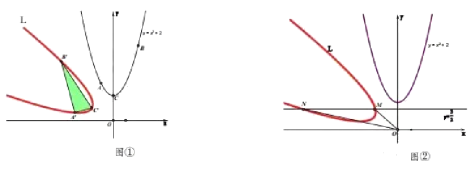
【题目】定义:在平面直角坐标系中,我们将函数![]() 的图象绕原点
的图象绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到的新曲线
后得到的新曲线![]() 称为“逆旋抛物线”.
称为“逆旋抛物线”.
(1)如图①,己知点![]() ,
,![]() 在函数
在函数![]() 的图象上,抛物线的顶点为
的图象上,抛物线的顶点为![]() ,若
,若![]() 上三点
上三点![]() 、
、![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 旋转后的对应点,连结
旋转后的对应点,连结![]() ,
,![]() 、
、![]() ,则
,则![]() __________;
__________;
(2)如图②,逆旋抛物线![]() 与直线
与直线![]() 相交于点
相交于点![]() 、
、![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com