【题目】已知关于x的一元二次方程。

（1）求证：方程有两个不相等的实数根；

（2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5。当△ABC是等腰三角形时，求k的值。

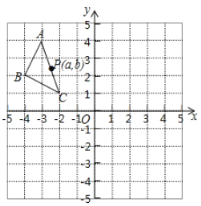
【题目】如图，在平面直角坐标系中，的三个顶点坐标为，，，绕原点逆时针旋转，得到，向右平移6个单位，再向上平移2个单位得到．

（1）画出和；

（2）是的边上一点，经旋转、平移后点的对应点分别为、，请写出点、的坐标．

【题目】如图，已知二次函数的图象与轴交于点，与轴的交点在和之间（不包括这两点），对称轴为直线.下列结论：①；②；③；④；⑤.其中正确的是________.

A.7B.8C.9D.10

【题目】如图，二次函数y=x2+bx+c的图象过点B（0，1）和C（4，3）两点，与x轴交于点D、点E，过点B和点C的直线与x轴交于点A．

(1)求二次函数的解析式；

(2)在x轴上有一动点P，随着点P的移动，存在点P使△PBC是直角三角形，请你求出点P的坐标；

(3)若动点P从A点出发，在x轴上沿x轴正方向以每秒2个单位的速度运动，同时动点Q也从A点出发，以每秒a个单位的速度沿射线AC运动，是否存在以A、P、Q为顶点的三角形与△ABD相似？若存在，直接写出a的值；若不存在，说明理由．

问题背景

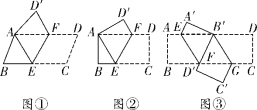
在数学活动课上，老师首先将平行四边形纸片ABCD按如图①所示方式折叠，使点C与点A重合，点D落到D′处，折痕为EF．这时同学们很快证得：△AEF是等腰三角形．接下来各学习小组也动手操作起来，请你解决他们提出的问题．

操作发现

(1) “争先”小组将矩形纸片ABCD按上述方式折叠，如图②，发现重叠部分△AEF恰好是等边三角形，求矩形ABCD的长、宽之比是多少？

实践探究

(2)“励志”小组将矩形纸片ABCD沿EF折叠，如图③，使B点落在AD边上的B′处；沿B′G折叠，使D点落在D′处，且B′D′过F点．试探究四边形EFGB′是什么特殊四边形？

(3)再探究：在图③中连接BB′，试判断并证明△BB′G的形状．

人类会作圆并且真正了解圆的性质是在2000多年前，由我国的墨子给出圆的概念：“一中同长也．”．意思说，圆有一个圆心，圆心到圆周的长都相等．这个定义比希腊数学家欧几里得给圆下的定义要早100年．与圆有关的定理有很多，弦切角定理就是其中之一．

我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．

弦切角定理：弦切角的度数等于它所夹弧所对的圆周角度数．

下面是弦切角定理的部分证明过程：

证明：如图①，AB与⊙O相切于点A．当圆心O在弦AC上时，容易得到∠CAB＝90°，所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数．

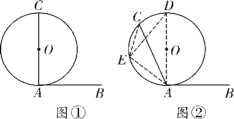
如图②，AB与⊙O相切于点A，当圆心O在∠BAC的内部时，过点A作直径AD交⊙O于点D，在上任取一点E，连接EC，ED，EA，则∠CED＝∠CAD．

…

任务：

(1)请按照上面的证明思路，写出该证明的剩余部分；

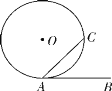
(2)如图③，AB与⊙O相切于点A．当圆心O在∠BAC的外部时，请写出弦切角定理的证明过程．

请你帮助该小组同学根据上表中的测量数据，求出交通指示牌CD的高度．(参考数据sin27°≈0.45，cos27°≈0.89，tan27°≈0.51，sin18°≈0.31，cos18°≈0.95，tan18°≈0.32)

【题目】运城有甲、乙两家葡萄采摘园的葡萄销售价格相同，中秋期间，两家采摘园推出优惠方案，甲园的优惠方案是：游客进园需购买门票，采摘的葡萄六折优惠；乙园的优惠方案是：游客进园不需购买门票，采摘园的葡萄按售价付款。优惠期间，设游客的葡萄采摘量为（千克），在甲园所需总费用为甲（元），在乙园所需总费用为乙（元），甲，乙与之间的函数关系如图所示．

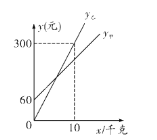
（1）求甲，乙与的函数表达式；

（2）在中秋期间，李娜一家三口准备去葡萄园采摘葡萄，采摘的葡萄合在一起支付费用，则李娜一家应选择哪家葡萄园更划算？

请根据统计图表中的信息解答下列问题：

(1)这次共抽取了________名参加演讲比赛的学生，统计图中a＝________，b＝________；

(2)若该校学生共有2000人，如果都参加了演讲比赛，请你估计成绩达到优秀的有多少人？

(3)若演讲比赛成绩为A等级的学生中恰好有2名女生，其余的学生为男生，从A等级的学生中抽取两名同学参加全市演讲比赛，求抽中一名男生和一名女生的概率．