
科目: 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线y![]() bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
(1)求抛物线的表达式及其顶点坐标;
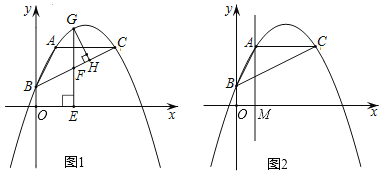
(2)如图1,点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,在点G运动的过程中,△GFH的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,过A点的直线垂直x轴于点M,点N为直线AM上任意一点,当△BCN为直角三角形时,请直接写出点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() ,D为直线BC上一点,E为直线AC上一点,
,D为直线BC上一点,E为直线AC上一点,![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,若点D在线段C上,点E在线段AC上,![]() ,
,![]() ,则
,则![]() ______
______![]() ;
;![]() ________
________![]() .
.
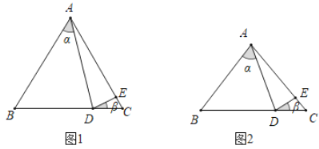
(2)如图2,若点D在线段BC上,点E在线段AC上,则![]() ,
,![]() 之间有什么关系式?它说明理由.
之间有什么关系式?它说明理由.
(3)是否存在不同于(2)中的![]() ,
,![]() 之间的关系式?请写出这个关系式(写出一种即可),说明理由:若不存在,请说明理由.
之间的关系式?请写出这个关系式(写出一种即可),说明理由:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某小区![]() 号楼对外销售,已知
号楼对外销售,已知![]() 号楼某单元共
号楼某单元共![]() 层,一楼为商铺,只租不售,二楼以上价格如下:第
层,一楼为商铺,只租不售,二楼以上价格如下:第![]() 层售价为
层售价为![]() 元/米
元/米![]() ,从第
,从第![]() 层起每上升一层,每平方米的售价提高
层起每上升一层,每平方米的售价提高![]() 元,反之每降一层,每平方米的售价降低
元,反之每降一层,每平方米的售价降低![]() 元,已知该单元每套的面积均为
元,已知该单元每套的面积均为![]() 米
米![]()
优惠活动
活动一:若一次性付清所有房款,降价![]() ,另免
,另免![]() 年物业费共
年物业费共![]() 元.
元.
活动二:若购买者一次性付清所有房款,降价![]() ,无赠送.
,无赠送.
(1)请在下表中,补充完整售价![]() (元/米
(元/米![]() )与楼层
)与楼层![]() (
(![]() 取正整数)之间的的数关系式.
取正整数)之间的的数关系式.
楼层 |
|
|
|
|
售价 | 不售 |
|
(2)某客户想购买该单元第![]() 层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算
层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一架无人机在距离地面高度为13.3米的点A处,测得地面点M的俯角为53°,这架无人机沿仰角为35°的方向飞行了55米到达点B,恰好在地面点N的正上方,M、N在同一水平线上求出M、N两点之间的距离.(结果精确到1米)
(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.)

查看答案和解析>>
科目: 来源: 题型:
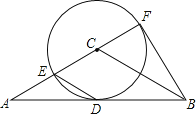
【题目】如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为点D,直线AC交⊙C于点E、F,且CF=![]() AC,
AC,
(1)求证:△ABF是直角三角形.
(2)若AC=6,则直接回答BF的长是多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解学生对排球、羽毛球、足球、篮球(以下分别用A、B、C、D表示)这四种球类运动的喜好情况.对全体学生进行了抽样调查(每位学生只能选一项最喜欢的运动),并将调查情况绘制成如下两幅不完整的统计图.
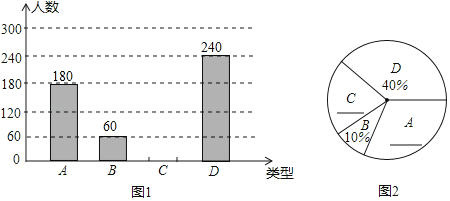
请根据以上信息回答下面问题:
(1)本次参加抽样调查的学生有 人.
(2)补全两幅统计图.
(3)若从本次参加抽样调查的学生中任取1人,则此人喜欢哪类球的概率最大?求其概率.
查看答案和解析>>
科目: 来源: 题型:
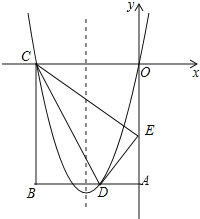
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com