
分析 (1)根据题意,将n 表示为n=a0×2k+a1×2k-1+a2×2k-2+…+ak-1×21+ak×20,实际是将十进制的数转化为二进制的数,
易得8=1×23+0×22+0×21+0×20,由I(n)的意义,可得答案;
(2)由组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.
解答 解:(1)根据题意,8=1×23+0×22+0×21+0×20,则I(8)=3;
(2)I(1)=0=0•2-1,I(2)+I(3)=1=1•20,
I(4)+I(5)+I(6)+I(7)=4=2•21,
I(8)+I(9)+…+I(15)=12=3•22…,
所以I(1)+I(2)+I(3)+…+I(2048)
=0•2-1+1•20+2•21+…+10•29+11
=9228.
故答案为:3,9228.
点评 本题考查了转化思想与二项式定理、等比数列的前n项和公式的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3>b3 | B. | a2<a3 | C. | a3<b3 | D. | b2>b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
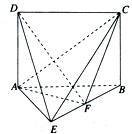 已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,AB=2,AD=$\sqrt{3}$,△ABE为等边三角形,平面ABCD⊥平面ABE,点F为棱BE的中点,
已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,AB=2,AD=$\sqrt{3}$,△ABE为等边三角形,平面ABCD⊥平面ABE,点F为棱BE的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com