
分析 (1)由题意设出直线l1的参数方程,代入椭圆方程,利用韦达定理求得tA•tB=-$\frac{8}{co{s}^{2}θ+4si{n}^{2}θ}$,由|PA|•|PB|=$\frac{8}{co{s}^{2}θ+4si{n}^{2}θ}$=$\frac{8}{1+3si{n}^{2}θ}$,根据正弦函数图象及性质即可求得|PA|•|PB|的最值;
(2)由l1⊥l2,求得l2的参数方程,并根据韦达定理求得|PC|•|PD|=丨tC•tD丨=$\frac{8}{1+3co{s}^{2}θ}$,表示出$\frac{1}{|PA||PB|}$+$\frac{1}{|PC||PD|}$,根据同角三角函数基本关系即可求证$\frac{1}{|PA||PB|}$+$\frac{1}{|PC||PD|}$为定值.
解答 解:(1)设直线l1的倾斜角为θ,则l1的参数方程为$\left\{\begin{array}{l}{x=2+tcosθ}\\{y=1+tsinθ}\end{array}\right.$(t为参数)
代入椭圆的方程$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$中,整理得:(cos2θ+4sin2θ)t2+(4cosθ+8sinθ)t-8=0,
∴由韦达定理可知:tA•tB=-$\frac{8}{co{s}^{2}θ+4si{n}^{2}θ}$,
∴|PA|•|PB|=$\frac{8}{co{s}^{2}θ+4si{n}^{2}θ}$=$\frac{8}{1+3si{n}^{2}θ}$,
故|PA|•|PB|的最大值为8,最小值为2.
证明:(2)∵l1⊥l2,不妨设l1的倾斜角小于l2的倾斜角,
则l2的倾斜角为$\frac{π}{2}$+θ,
因此直线l2的参数方程为$\left\{\begin{array}{l}{x=2+tcos(\frac{π}{2}+θ)}\\{y=1+tsin(\frac{π}{2}+θ)}\end{array}\right.$(t为参数)
代入椭圆的方程$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1,
整理得:(sin2θ+4cos2θ)t2+4(2cosθ-sinθ)t-8=0,
∴|PC|•|PD|=丨tC•tD丨=$\frac{8}{1+3co{s}^{2}θ}$,
∴$\frac{1}{|PA||PB|}$+$\frac{1}{|PC||PD|}$=$\frac{1+3si{n}^{2}θ}{8}$+$\frac{1+3co{s}^{2}θ}{8}$=$\frac{5}{8}$,
∴$\frac{1}{|PA||PB|}$+$\frac{1}{|PC||PD|}$为定值.
点评 本题考查直线的参数方程,直线与椭圆的位置关系,韦达定理及正弦函数图象及性质,考查转化思想,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
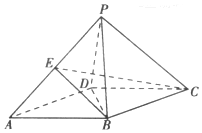 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=$\sqrt{6}$.
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com