
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
分析 利用诱导公式化简三角函数式,再利用二次函数的性质求得它的最大值.
解答 解:∵x∈(0,$\frac{π}{4}$),则函数f(x)=$\frac{cos(π-x)sin(π+x)-co{s}^{2}(\frac{π}{2}+x)}{si{n}^{2}(\frac{π}{2}-x)}$=$\frac{-cosx•(-sinx){-sin}^{2}x}{{cos}^{2}x}$=tanx-tan2x=$\frac{1}{4}$-${(tanx-\frac{1}{2})}^{2}$,
故当tanx=$\frac{1}{2}$时,函数f(x)取得最大值为$\frac{1}{4}$,
故选:C.
点评 本题主要考查应用诱导公式化简三角函数式,二次函数的性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
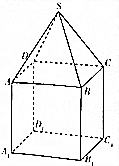 如图,ABCD-A1B1C1D1是边长为1的正方体,S-ABCD是高为1的正四棱锥,若点S,A1,B1,C1,D1在同一个球面上,则该球的表面积为$\frac{81}{16}π$.
如图,ABCD-A1B1C1D1是边长为1的正方体,S-ABCD是高为1的正四棱锥,若点S,A1,B1,C1,D1在同一个球面上,则该球的表面积为$\frac{81}{16}π$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com