练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某几何体的三视图如图所示（单位：cm），则该几何体的侧面PAB的面积是（　　）
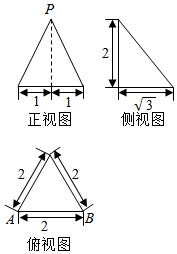
    A．$\sqrt{3}$B．2C．$\sqrt{5}$D．$\sqrt{7}$

    分析 由三视图可知：该几何体是一个三棱锥，底面是一个正三角形，后面的侧棱与底面垂直．

    解答 解：由三视图可知：该几何体是一个三棱锥，底面是一个正三角形，后面的侧棱与底面垂直．
    ∴该几何体的侧面PAB的面积=$\frac{1}{2}×2×\sqrt{{2}^{2}+（\sqrt{3}）^{2}}$=$\sqrt{7}$．
    故选：D．

    点评 本题考查了三视图的有关计算、三棱锥的侧面积的计算公式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=$\frac{1}{2}$x2-3x+（a-1）lnx，g（x）=ax，h（x）=f（x）-g（x）+3x．
    （1）当a=5时，求函数f（x）的导函数f′（x）的最小值；
    （2）当a=3时，求函数h（x）的单调区间及极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD⊥AB，AB∥DC，PA⊥底面ABCD，点E为棱PC的中点．AD=DC=AP=2AB=2．
    （1）证明：BE⊥平面PDC；
    （2）若F为棱PC上一点，满足BF⊥AC，求二面角F-AD-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

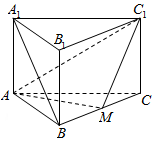    20．如图，已知三棱柱A1B1C1-ABC中，侧棱与底面垂直，AB=BC=AA1，∠ABC=90°，M是BC的中点．
    （1）求证：A1B∥平面AMC1；
    （2）求平面A1B1M与平面AMC1所成角的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．一艘船在航行过程中发现前方的河道上有一座圆拱桥．在正常水位时，拱桥最高点距水面8m，拱桥内水面宽32m，船只在水面以上部分高6.5m，船顶部宽8m，故通行无阻，如图所示．
    （1）建立适当的平面直角坐标系，求正常水位时圆弧所在的圆的方程；
    （2）近日水位暴涨了2m，船已经不能通过桥洞了．船员必须加重船载，降低船身在水面以上的高度，试问：船身至少降低多少米才能通过桥洞？（精确到0.1m，$\sqrt{6}≈2.45$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

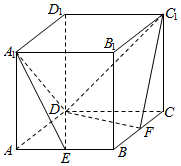    17．如图，在正方体ABCD-A1B1C1D1中，E，F分别是棱AB、BC的中点，则平面A1DE与平面C1DF所成二面角的余弦值为（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{1}{2}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

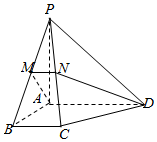    4．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，PA=AD=AB=2BC=2，过AD的平面分别交PB，PC于M，N两点．
    （Ⅰ）求证：MN∥BC；
    （Ⅱ）若M，N分别为PB，PC的中点，
    ①求证：PB⊥DN；
    ②求二面角P-DN-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD，且AE⊥平面CDE，AE=1．
    （Ⅰ）求证：平面ABCD⊥平面ADE；
    （Ⅱ）设点F是棱BC上一点，若二面角A-DE-F的余弦值为$\frac{{\sqrt{10}}}{10}$，试确定点F在BC上的位置．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某小学为迎接校运动会的到来，在三年级招募了16名男志愿者和14名女志愿者．调查发现，男、女志愿者中分别各有10人和6人喜欢运动，其他人员不喜欢运动．
    （Ⅰ）根据以上数据完成以下2×2列联表：
    喜欢运动不喜欢运动总计
    男a=b=
    女c=d=
    总计n=
    （Ⅱ）判断性别与喜欢运动是否有关，并说明理由．
    （Ⅲ）如果喜欢运动的女志愿者中恰有4人懂得医疗救护，现从喜欢运动的女志愿者中抽取2名负责医疗救护工作，求抽出的2名志愿者都懂得医疗救护的概率．
    附：${Χ^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}（{n=a+b+c+d}）$
    临界值表（部分）：
    P（χ2≥x0）0.0500.0250.0100.001
    x03.8415.0246.63510.828

    查看答案和解析>>

    同步练习册答案