

分析 根据题意,求出积分的上下限,利用定积分的几何意义表示图形面积,然后计算即可
解答 解:令y=x2-x=0,解得x=0或x=1,
故由直线x=-2,x=2,y=0及曲线y=x2-x所围成的图形的面积
S=${∫}_{-2}^{0}$(x2-x)dx-${∫}_{0}^{1}$(x2-x)dx+${∫}_{1}^{2}$(x2-x)dx,
=($\frac{1}{3}$x3-$\frac{1}{2}$x2)|${\;}_{-2}^{0}$-($\frac{1}{3}$x3$\frac{1}{2}$x2)|${\;}_{0}^{1}$+($\frac{1}{3}$x3-$\frac{1}{2}$x2)|${\;}_{1}^{2}$,
=0-(-$\frac{8}{3}$-2)-($\frac{1}{3}$-$\frac{1}{2}$-0)+($\frac{8}{3}$-2)-($\frac{1}{3}$-$\frac{1}{2}$)
=$\frac{17}{3}$
点评 本题考查利用定积分的几何意义求曲边梯形的面积;明确意义后确定积分的上限和下限是关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,0)∪(0,1) | C. | (-∞,0)∪(0,2) | D. | (-1,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x={t^{\frac{1}{2}}}\\ y={t^{-\frac{1}{2}}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x={2^t}\\ y={2^{-t}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=log_2t\\ y=log_t2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=sinα\\ y=\frac{1}{sinα}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
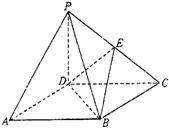 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{101}{100}$ | B. | $\frac{200}{101}$ | C. | $\frac{99}{100}$ | D. | $\frac{101}{200}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com