
【题目】若关于x的方程22x+2xa+a+1=0有实根,求实数a的取值范围.
【答案】解:法一:(换元法)
设t=2x(t>0),则原方程可变为t2+at+a+1=0,(*)
原方程有实根,即方程(*)有正根.
令f(t)=t2+at+a+1.
①若方程(*)有两个正实根t1 , t2 ,
则 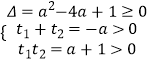 解得-1<a≤2-2
解得-1<a≤2-2 ![]() ;
;
②若方程(*)有一个正实根和一个负实根(负实根,不合题意,舍去),则f(0)=a+1<0,解得a<-1;
③当a=-1时,t=1,x=0符合题意.
综上可知实数a的取值范围是(-∞,2-2 ![]() ].
].
法二:(分离变量法)
由方程,解得a=- ![]() ,设t=2x(t>0),
,设t=2x(t>0),
则a=- ![]() =-
=- ![]()
=2- ![]() ,其中t+1>1,
,其中t+1>1,
由基本(均值)不等式,得(t+1)+ ![]() ≥2
≥2 ![]() ,当且仅当t=
,当且仅当t= ![]() -1时取等号,故a≤2-2
-1时取等号,故a≤2-2 ![]() .
.
综上可知实数a的取值范围是(-∞,2-2 ![]() ].
].
【解析】先换元,令t=2x , 则关于 t 方程为t2+at+a+1=0 有实根,令![]() ,结合基本不等式即可解出实数m的取值范围.或者用分离参数,利用基本不等式,即可求得实数m的取值范围.
,结合基本不等式即可解出实数m的取值范围.或者用分离参数,利用基本不等式,即可求得实数m的取值范围.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(1)求数列{an}和{bn}的通项公式;
(2)令cn=anbn , 设数列{cn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R, ![]() +1>3x0”的否定是“x∈R,x2+1≤3x”;
+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量a与b的夹角是钝角”的充要条件是“a·b<0”.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在矩形 ![]() 中,
中, ![]() ,
, ![]() 是
是 ![]() 的中点,将三角形
的中点,将三角形 ![]() 沿
沿 ![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面 ![]()
![]() 平面
平面 ![]() .
.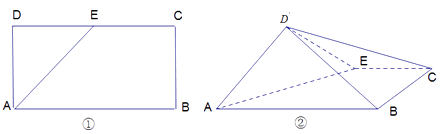
(1)在线段 ![]() 上确定点
上确定点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并证明;
,并证明;
(2)求 ![]() 与
与 ![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两个不同点 ![]() 、
、 ![]() 满足条件:①
满足条件:① ![]() 、
、 ![]() 都在函数
都在函数 ![]() 的图像上;②
的图像上;② ![]() 、
、 ![]() 关于原点对称,则称点对
关于原点对称,则称点对 ![]() 是函数
是函数 ![]() 的一对“友好点对”(注:点对
的一对“友好点对”(注:点对 ![]() 与
与 ![]() 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数 ![]()
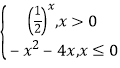 ,则此函数的“友好点对”有( )对.
,则此函数的“友好点对”有( )对.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c,d都是常数,a>b,c>d.若f(x)=2 017-(x-a)(x-b)的零点为c,d,则下列不等式正确的是( )
A.a>c>b>d
B.a>b>c>d
C.c>d>a>b
D.c>a>b>d
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“抛物线 ![]() 的准线方程为
的准线方程为 ![]() ”是“抛物线
”是“抛物线 ![]() 的焦点与双曲线
的焦点与双曲线 ![]() 的焦点重合”的( )
的焦点重合”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆 ![]() 经过点
经过点 ![]() ,并且与圆
,并且与圆 ![]() 相切.
相切.
(1)求点P的轨迹C的方程;
(2)设 ![]() 为轨迹C内的一个动点,过点
为轨迹C内的一个动点,过点 ![]() 且斜率为
且斜率为 ![]() 的直线
的直线 ![]() 交轨迹C于A,B两点,当k为何值时?
交轨迹C于A,B两点,当k为何值时? ![]() 是与m无关的定值,并求出该值定值.
是与m无关的定值,并求出该值定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com