练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）= ﹣k（ +lnx），若x=2是函数f（x）的唯一一个极值点，则实数k的取值范围为（ ）
    A.（﹣∞，e]
    B.[0，e]
    C.（﹣∞，e）
    D.[0，e）

    【答案】C
    【解析】解：∵函数f（x）= ﹣k（ +lnx），

    ∴函数f（x）的定义域是（0，+∞）

    ∴f′（x）= ﹣k（﹣ + ）=

    ∵x=2是函数f（x）的唯一一个极值点

    ∴x=2是导函数f′（x）=0的唯一根．

    ∴ex﹣kx=0在（0，+∞）无变号零点，

    令g（x）=ex﹣kx

    g′（x）=ex﹣k①k≤0时，g′（x）＞0恒成立．g（x）在（0，+∞）时单调递增的

    g（x）的最小值为g（0）=1，g（x）=0无解②k＞0时，g′（x）=0有解为：x=lnk

    0＜x＜lnk时，g′（x）＜0，g（x）单调递减

    lnk＜x时，g′（x）＞0，g（x）单调递增

    ∴g（x）的最小值为g（lnk）=k﹣klnk

    ∴k﹣klnk＞0

    ∴k＜e，

    由y=ex和y=ex图象，它们切于（1，e），

    综上所述，k≤e．

    故选C

    由f（x）的导函数形式可以看出，需要对k进行分类讨论来确定导函数为0时的根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=lnx﹣ax+1，其中a为常实数．
    （1）讨论函数f（x）的单调性；
    （2）当a=1时，求证：f（x）≤0；
    （3）当n≥2，且n∈N*时，求证： ＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：如果函数f（x）在[a，b]上存在x1 ， x2（a＜x1＜x2＜b）满足 ， ，则称函数f（x）是[a，b]上的“双中值函数”．已知函数f（x）=x3﹣x2+a是[0，a]上的“双中值函数”，则实数a的取值范围是（ ）
    A.
    B.（ ）
    C.（ ，1）
    D.（ ，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点P(2，－1)．

    (1)求过P点且与原点距离为2的直线l的方程；

    (2)求过P点且与原点距离最大的直线l的方程，最大距离是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=xlnx，g（x）=﹣x2+ax﹣3．
    （1）求函数f（x）在[t，t+2]（t＞0）上的最小值；
    （2）对一切x∈（0，+∞），2f（x）≥g（x）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD－A1B1C1D1的棱长为a，M为BD1的中点，N在A1C1上，且满足|A1N|＝3|NC1|.

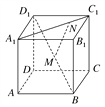
    (1)求MN的长；

    (2)试判断△MNC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆 =1（a＞b＞0），F1、F2分别为椭 圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B、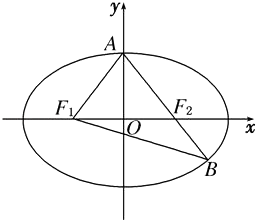

    （1）若∠F1AB=90°，求椭圆的离心率；
    （2）若 =2 ， = ，求椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=90°，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG.

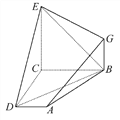
    (1)求证：EC⊥CD.

    (2)求证：AG∥平面BDE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知A(0,0)，B(1,0)，C(2,1)，D(0,3)，将四边形ABCD绕y轴旋转一周，求所得旋转体的表面积和体积.

    查看答案和解析>>

    同步练习册答案