
| A. | 命题①,②均为真命题 | B. | 命题②,③均为假命题 | ||
| C. | 命题②,④均为假命题 | D. | 命题①,③,④均为真命题 |
分析 先根据直角距离的定义分别表示出所求的问题的表达式,然后根据集合中绝对值的性质进行判定即可.
解答 解:①已知P(1,2),Q(cos2θ,sin2θ)(θ∈R),则d(P,Q)=|1-cos2θ|+|2-sin2θ|=sin2θ+2-sin2θ=2为定值;故①正确,
②已知P,Q,R三点不共线,设P(1,0),Q(0,0),R(0,1),
则d(P,Q)=|xP-xQ|+|yP-yQ|=1,
d(Q,R)=|xQ-xR|+|yQ-yR|=1.
d(P,R)=|xP-xR|+|yP-yR|=1+1=2,此时d(P,Q)+d(Q,R)=d(P,R);
∴d(P,Q)+d(Q,R)>d(P,R)不成立,故②错误,
③若|PQ|表示P、Q两点间的距离,那么|PQ|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$,d(P,Q)=|x1-x2|+|y1-y2|,
∵2(a2+b2)≥(a+b)2,
∴$\sqrt{2[({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}]}$≥|x1-x2|+|y1-y2|,即$\sqrt{2}$|PQ|≥d(P,Q),
则|PQ|≥$\frac{1}{\sqrt{2}}$d(P,Q)=$\frac{\sqrt{2}}{2}$d(P,Q),故③正确,
④若P,Q是$\frac{x^2}{5}+\frac{y^2}{4}$=1上的任意两点,d(P,Q)的最大,设P($\sqrt{5}$cosα,2sinα),Q(-$\sqrt{5}$cosα,-2sinα);则d(P,Q)=|x1-x2|+|y1-y2|=2($\sqrt{5}$cosα+2sinα)=6sin(α+θ),则d(P,Q)的最大值为6;故④正确,
故选:D
点评 本题考查两点之间的“直角距离”的定义,绝对值的意义,关键是明确P(x1,y1)、Q(x2,y2)两点之间的“直角距离”的含义.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
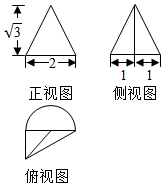
| A. | 4+$\frac{3π}{2}$ | B. | 4+3π | C. | 4+π | D. | 4+$\sqrt{3}$+$\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢户外运动 | 不喜欢户外运动 | 合计 | |
| 男员工 | 5 | ||
| 女员工 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$$\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{BD}$ | B. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{5}{6}$$\overrightarrow{BD}$ | C. | -$\frac{5}{6}$$\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{BD}$ | D. | $\frac{5}{6}$$\overrightarrow{AC}$-$\frac{1}{6}$$\overrightarrow{BD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com