数列{an}中,a1=1,且an+1=Sn(n≥1,n∈N*),数列{bn}是等差数列,其公差d>0,b1=1,且b3、b7+2、3b9成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{an+bn}的前n项和Tn.
解:(1)由已知有S
n+1-S
n=S
n,即S
n+1=2S
n(n∈N
*),
∴{S
n}是以S
1=a
1=1为首项,2为公比的等比数列,∴S
n=2
n-1,
∴n≥2时,a
n=S
n-1=2
n-2,
∵a
1=1,不满足上式,∴a
n=
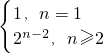
;
∵b
3,b
7+2,3b
9成等比数列,
∴(b
7+2)
2=b
3•3b
9,即(1+6d+2)
2=(1+2d)•3(1+8d),
解得d=1或d=-

(舍),
∴b
n=1+(n-1)×1=n;
(2)n=1时,T
1=a
1+b
1=2
n≥2时,T
n=a
n+b
n=(1+1+2+…+2
n-2)+(1+2+…+n)=1+
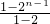
+

=
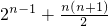
综上,T
n=
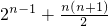
.
分析:(1)先确定{S
n}的通项,再由a
n+1=S
n,得数列{a
n}通项公式,利用数列{b
n}是等差数列,其公差d>0,b
1=1,且b
3、b
7+2、3b
9成等比数列,求出数列{b
n}的公差,可求得数列{b
n}的通项公式;
(2)分类讨论,再分组求和,即可求数列{a
n+b
n}的前n项和T
n.
点评:本题考查数列的通项与求和,考查数列递推式,考查学生的计算能力,确定数列的通项是关键.

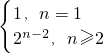 ;
; (舍),
(舍),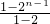 +
+ =
=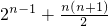
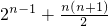 .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案