
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
【答案】(1)0. 016;(2)![]()
【解析】试题分析:(1)根据频率等于频数除以总数,可得到参加校生物竞赛的人数,再根据分数在[80,90)之间的频率求频数,根据矩形高等于对应频率除以组距得高(2)先根据枚举法列出所有基本事件,再计数至少有1人分数在[90,100]之间基本试卷数,最后根据古典概型概率公式求概率
试题解析: (1)因为分数在[50,60)之间的频数为2,频率为0. 008×10=0. 08,所以高一(1)班参加校生物竞赛的人数为![]() =25.
=25.
分数在[80,90)之间的频数为25-2-7-10-2=4,频率为![]() =0. 16,
=0. 16,
所以频率分布直方图中[80,90)间的矩形的高为![]() =0. 016.
=0. 016.
(2)设“至少有1人分数在[90,100]之间”为事件A,将[80,90)之间的4人编号为1、2、3、4,[90,100]之间的2人编号为5、6.
在[80,100]之间任取2人的基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个.其中,至少有1人分数在[90,100]之间的基本事件有9个,
根据古典概型概率的计算公式,得P(A)=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
, .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上,则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() ,
,![]() ,则称
,则称![]() 是
是![]() 的“收缩数列”.其中
的“收缩数列”.其中![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() 且
且![]() ,
,![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若曲线
,若曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() ,不等式
,不等式![]() 的解集为非空集合
的解集为非空集合![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求![]() 的解析式,并用
的解析式,并用![]() 表示
表示![]() ;
;
(Ⅱ)若任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
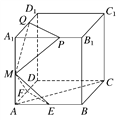
【题目】已知棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别是线段AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x(0<x<1).设平面MEF∩平面MPQ
=l,现有下列结论:
①l∥平面ABCD;
②l⊥AC;
③直线l与平面BCC1B1不垂直;
④当x变化时,l不是定直线.
其中不成立的结论是________.(写出所有不成立结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为
为![]() 椭圆上一点,且
椭圆上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程及
的方程及![]() 的值;
的值;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围.
的离心率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com