
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
, .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
科目:高中数学 来源: 题型:
【题目】有下列命题:(1)双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;(2)“
有相同的焦点;(2)“![]() ”是“
”是“![]() ”的必要不充分条件;(3)若向量
”的必要不充分条件;(3)若向量![]() 与向量
与向量![]() 共线,则向量
共线,则向量![]() ,
,![]() 所在直线平行;(4)若
所在直线平行;(4)若![]()
![]()
![]() 三点不共线,
三点不共线,![]() 是平面
是平面![]() 外一点,
外一点,![]() ,则点
,则点![]() 一定在平面
一定在平面![]() 上;其中是真命题的是______(填上正确命题的序号)
上;其中是真命题的是______(填上正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的宣传费
(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]()
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
(1)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为年销售量
,哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() ,根据(2)的结果回答:当年宣传费
,根据(2)的结果回答:当年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占![]() 、家占
、家占![]() 、个人空间占
、个人空间占![]() .如下表:
.如下表:
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计数据表明,样本中所有人每天用于阅读的时间(简称阅读用时)都不超过3小时,其频数分布表如下:(用时单位:小时)
用时分组 |
|
|
|
|
|
|
频数 | 10 | 20 | 50 | 60 | 40 | 20 |
(1)用样本估计总体,求该市市民每天阅读用时的平均值;
(2)为引导市民积极参与阅读,有关部门牵头举办市读书经验交流会,从这200人中筛选出男女代表各3名,其中有2名男代表和1名女代表喜欢古典文学.现从这6名代表中任选2名男代表和2名女代表参加交流会,求参加交流会的4名代表中,喜欢古典文学的男代表多于喜欢古典文学的女代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中![]() 为实数集,
为实数集,![]() 为有理数集,则关于函数
为有理数集,则关于函数![]() 有如下四个命题:①
有如下四个命题:①![]() ;②函数
;②函数![]() 是偶函数;③任取一个不为零的有理数
是偶函数;③任取一个不为零的有理数![]() ,
,![]() 对任意的
对任意的![]() 恒成立;④存在三个点
恒成立;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中真命题的个数有( )
为等边三角形.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
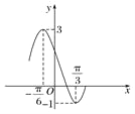
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com