
【题目】已知椭圆C:![]() (a>b>0)的右焦点为F(1,0),且点P
(a>b>0)的右焦点为F(1,0),且点P![]() 在椭圆C上,O为坐标原点.
在椭圆C上,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设过定点T(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角,求直线l的斜率k的取值范围.
【答案】(1)![]() +
+![]() =1(2)
=1(2)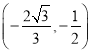 ∪
∪
【解析】
(1)由c=1得a2=b2+1,再代入P点坐标可求得a,b;
(2)设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),直线方程与椭圆方程联立消元得![]() 的一元二次方程,其判别式需大于0,由韦达定理得
的一元二次方程,其判别式需大于0,由韦达定理得![]() ,条件∠AOB为锐角对应
,条件∠AOB为锐角对应![]() ,代入
,代入![]() 后可求得
后可求得![]() 的范围.
的范围.
(1)由题意得c=1,所以a2=b2+1,①
又点P![]() 在椭圆C上,所以
在椭圆C上,所以![]() +
+![]() =1,②
=1,②
由①②可解得a2=4,b2=3,
所以椭圆C的标准方程为![]() +
+![]() =1.
=1.
(2)设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),由 得(4k2+3)x2+16kx+4=0,
得(4k2+3)x2+16kx+4=0,
因为Δ=16(12k2-3)>0,所以k2>![]() ,则x1+x2=
,则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因为∠AOB为锐角,所以![]() ·
·![]() >0,即x1x2+y1y2>0,所以x1x2+(kx1+2)(kx2+2)>0,
>0,即x1x2+y1y2>0,所以x1x2+(kx1+2)(kx2+2)>0,
所以(1+k2)x1x2+2k(x1+x2)+4>0,即(1+k2)·![]() +2k·
+2k·![]() +4>0,
+4>0,
解得k2<![]() .又k2>
.又k2>![]() ,所以
,所以![]() <k2<
<k2<![]() ,解得-
,解得-![]() <k<-
<k<-![]() 或
或![]() <k<
<k<![]() .
.
所以直线l的斜率k的取值范围为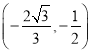 ∪
∪


科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
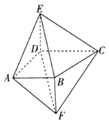
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
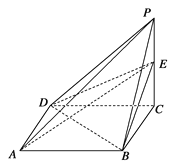
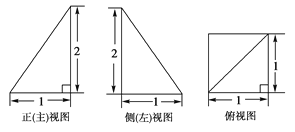
(1)求证:BD⊥AE
(2)若点E为PC的中点,求二面角D-AE-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() (万元),若年产量不足
(万元),若年产量不足![]() 千件,
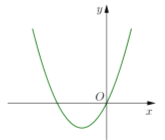
千件, ![]() 的图像是如图的抛物线,此时
的图像是如图的抛物线,此时![]() 的解集为
的解集为![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年产量不小于
,若年产量不小于![]() 千件,
千件, ![]() ,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集.整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频率分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
b.国家创新指数得分在![]() 这一组的是:61.7,62.4,63.6,65.9,66.4,68.5,69.1,69.3,69.5.
这一组的是:61.7,62.4,63.6,65.9,66.4,68.5,69.1,69.3,69.5.
c.40个国家的人均国内生产总值(万美元)和国家创新指数得分情况统计图:
d.中国的国家创新指数得分为69.5,人均国内生产总值9960美元.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,解答下列问题:
(1)中国的国家创新指数得分排名世界第几?
(2)是否有99.9%的把握认为“人均国内生产总值影响国家创新指数得分”?
(3)用(1)(2)得到的结论,结合所学知识.合理解释d中客观存在的数据.
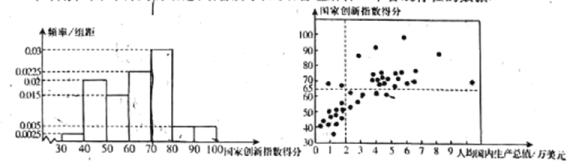
附: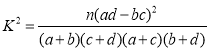 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
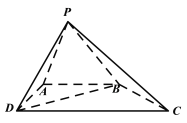
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com