
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
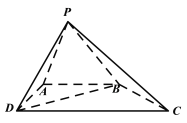
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)见证明;(2)见解析
【解析】
(1)利用余弦定理计算BC,根据勾股定理可得BC⊥BD,结合BC⊥PD得出BC⊥平面PBD,于是平面PBD⊥平面PBC;(2)建立空间坐标系,设![]() λ,计算平面ABM和平面PBD的法向量,令法向量的夹角的余弦值的绝对值等于
λ,计算平面ABM和平面PBD的法向量,令法向量的夹角的余弦值的绝对值等于![]() ,解方程得出λ的值,即可得解.
,解方程得出λ的值,即可得解.
(1)证明:因为四边形![]() 为直角梯形,
为直角梯形,
且![]() ,
, ![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() 。根据余弦定理得
。根据余弦定理得![]()
所以![]() ,故
,故![]() .
.
又因为![]() ,
, ![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面PBC,所以
平面PBC,所以![]()
(2)由(1)得平面![]() 平面
平面![]() ,
,
设![]() 为
为![]() 的中点,连结
的中点,连结![]() ,因为
,因为![]() ,
,
所以![]() ,
,![]() ,又平面
,又平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
如图,以![]() 为原点分别以
为原点分别以![]() ,
,![]() 和垂直平面
和垂直平面![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() ,
,
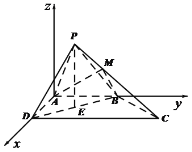
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
假设存在![]() 满足要求,设
满足要求,设![]() ,即
,即![]() ,
,
所以![]() ,
,
易得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,![]() ,
, ![]()
由 得
得![]() ,不妨取
,不妨取![]() .
.
因为平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,所以
,所以![]() ,
,
解得![]() ,(不合题意舍去).
,(不合题意舍去).
故存在![]() 点满足条件,且
点满足条件,且![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C的顶点是原点O,以x轴为对称轴,且经过点P(1,2).
(1)求抛物线C的方程;
设点A,B在抛物线C上,直线PA,PB分别与y轴交于点M,N,|PM|=|PN|.求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线斜率为2,试求a的值及此时的切线方程;
处的切线斜率为2,试求a的值及此时的切线方程;
(2)若函数![]() 在区间
在区间![]() (其中
(其中![]() …为自然对数的底数)上有唯一的零点,求实数a的取值范围.
…为自然对数的底数)上有唯一的零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某药业公司统计了2010-2019年这10年某种疾病的患者人数,结论如下:该疾病全国每年的患者人数都不低于100万,其中有3年的患者人数低于200万,有6年的患者人数不低于200万且低于300万,有1年的患者人数不低于300万.
(1)药业公司为了解一新药品对该疾病的疗效,选择了200名患者,随机平均分为两组作为实验组和对照组,实验结束时,有显著疗效的共110人,实验组中有显著疗效的比率为70%.请完成如下的2×2列联表,并根据列联表判断是否有99.9%把握认为该药品对该疾病有显著疗效;
实验组 | 对照组 | 合计 | |
有显著疗效 | |||
无显著疗效 | |||
合计 | 200 |
(2)药业公司最多能引进3条新药品的生产线,据测算,公司按如下条件运行生产线:
该疾病患者人数(单位:万) |
|
|
|
最多可运行生产线数 | 1 | 2 | 3 |
每运行一条生产线,可产生年利润6000万元,没运行的生产线毎条每年要亏损1000万元.根据该药业公司这10年的统计数据,将患者人数在以上三段的频率视为相应段的概率、假设各年的患者人数相互独立.欲使该药业公司年总利润的期望值达到最大,应引进多少条生产线?
附:参考公式: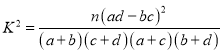 ,其中
,其中![]() .
.
| 0.05 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,a1=1,且4Sn,3Sn+1,2Sn+2成等差数列.
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=0,bn+1﹣bn=1,设cn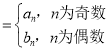 ,求数列{cn}的前2n项和.
,求数列{cn}的前2n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节是我国民间为纪念爱国诗人屈原的一个传统节日.某市为了解端午节期间粽子的销售情况,随机问卷调查了该市1000名消费者在去年端午节期间的粽子购买量(单位:克),所得数据如下表所示:
购买量 |
|
|
|
|
|
人数 | 100 | 300 | 400 | 150 | 50 |
将烦率视为概率
(1)试求消费者粽子购买量不低于300克的概率;
(2)若该市有100万名消费者,请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求(以各区间中点值作为该区间的购买量).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com