
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线斜率为2,试求a的值及此时的切线方程;
处的切线斜率为2,试求a的值及此时的切线方程;
(2)若函数![]() 在区间
在区间![]() (其中
(其中![]() …为自然对数的底数)上有唯一的零点,求实数a的取值范围.
…为自然对数的底数)上有唯一的零点,求实数a的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据导数的几何意义求解即可;
(2)讨论参数![]() 的值,确定函数
的值,确定函数![]() 在区间
在区间![]() 的单调性,从而根据零点的个数,得出实数a的取值范围.
的单调性,从而根据零点的个数,得出实数a的取值范围.
(1)由![]() ,(
,(![]() ).
).
由已知![]() .
.
可得:![]()
又此时![]() .
.
所以所求的切线方程为:![]() .
.
即:![]()
(2)![]() ,其中
,其中![]()
①当![]() 时,
时,![]() 在区间
在区间![]() 恒成立,
恒成立,![]() 在区间
在区间![]() 单调递增
单调递增
又∵![]() ,∴函数
,∴函数![]() 在区间
在区间![]() 上有唯一的零点,符合题意.
上有唯一的零点,符合题意.
②当![]() 时,
时,![]() 在区间
在区间![]() 恒成立,
恒成立,![]() 在区间
在区间![]() 单调递减
单调递减
又∵![]() ,∴函数
,∴函数![]() 在区间
在区间![]() 上有唯一的零点,符合题意.
上有唯一的零点,符合题意.
③当![]() 时
时
(i)![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
又∵![]() ,
,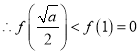 ,∴函数
,∴函数![]() 在区间
在区间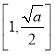 上有唯一的零点
上有唯一的零点
(ii)当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
∴要使![]() 在区间
在区间![]() 上有唯一的零点,只有当
上有唯一的零点,只有当![]() 时符合题意
时符合题意
即![]() ,即
,即![]()
∴![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有唯一的零点;
上有唯一的零点;
∴综上a的取值范围是![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上贏得一片赞誉.我国某口罩生产厂商在加大生产的同时.狠抓质量管理,不定时抽查口罩质量,该厂质检人员从某日所生产的口罩中随机抽取了100个,将其质量指标值分成以下五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
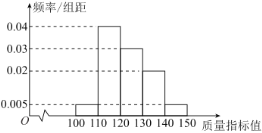
(1)规定:口罩的质量指标值越高,说明该口罩质量越好,其中质量指标值低于130的为二级口罩,质量指标值不低于130的为一级口罩.现从样本口罩中利用分层抽样的方法随机抽取8个口罩,再从中抽取3个,记其中一级口罩个数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在2020年“五一”劳动节前,甲,乙两人计划同时在该型号口罩的某网络购物平台上分别参加![]() 、
、![]() 两店各一个订单“秒杀”抢购,其中每个订单由
两店各一个订单“秒杀”抢购,其中每个订单由![]() 个该型号口罩构成.假定甲、乙两人在
个该型号口罩构成.假定甲、乙两人在![]() 、
、![]() 两店订单“秒杀”成功的概率分别为
两店订单“秒杀”成功的概率分别为![]() ,
,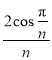 ,记甲、乙两人抢购成功的订单总数量、口罩总数量分别为
,记甲、乙两人抢购成功的订单总数量、口罩总数量分别为![]() ,
,![]() ,
,
①求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②求当![]() 的数学期望
的数学期望![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,电商行业的蓬勃发展带动了快递业的迅速增长,快递公司揽收价格一般是采用“首重+续重”的计价方式.首重是指最低的计费重量,续重是指超过首重部分的计费重量,不满一公斤按一公斤计费.某快递网点将快件的揽收价格定为首重(不超过一公斤)8元,续重2元/公斤(例如,若一个快件的重量是0.6公斤,按8元计费;若一个快件的重量是1.4公斤,按![]() 元
元![]() 元
元![]() 元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
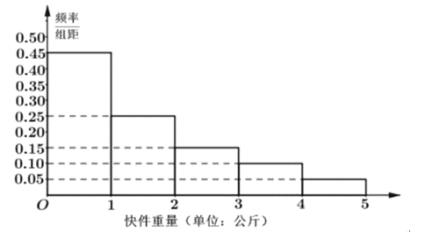
(1)根据样本估计总体的思想,将频率视作概率,求该网点揽收快件的平均价格;
(2)为了获得更大的利润,该网点对“一天中收发一件快递的平均成本![]() (单位:元)与当天揽收的快递件数
(单位:元)与当天揽收的快递件数![]() (单位:百件)
(单位:百件)![]() 之间的关系”进行调查研究,得到相关数据如下表:
之间的关系”进行调查研究,得到相关数据如下表:
每天揽收快递件数 | 2 | 3 | 4 | 5 | 8 |
每件快递的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
根据以上数据,技术人员分别根据甲、乙两种不同的回归模型,得到两个回归方程:
方程甲:![]() ,方程乙:
,方程乙:![]() .
.
①为了评价两种模型的拟合效果,根据上表数据和相应回归方程,将以下表格填写完整(结果保留一位小数),分别计算模型甲与模型乙的残差平方和![]() ,
,![]() ,并依此判断哪个模型的拟合效果更好(备注:
,并依此判断哪个模型的拟合效果更好(备注:![]() 称为相应于点
称为相应于点![]() 的残差,残差平方和
的残差,残差平方和![]() ;
;
每天揽收快递件数 | 2 | 3 | 4 | 5 | 8 | |
每天快递的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
模型甲 | 预报值 | 5.2 | 5.0 | 4.8 | ||
残差 |
| 0.2 | 0.4 | |||
模型乙 | 预报值 | 5.5 | 4.8 | 4.5 | ||
预报值 |
| 0 | 0.1 | |||
②预计该网点今年6月25日(端午节)一天可以揽收1000件快递,试根据①中确定的拟合效果较好的回归模型估计该网点当天的总利润(总利润=(平均价格-平均成本)×总件数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,与圆
,与圆![]() 有且只有两个公共点.
有且只有两个公共点.
(1)求抛物线![]() 的方程;
的方程;
(2)经过![]() 的动直线
的动直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,试问在直线
两点,试问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得直线
,使得直线![]() 的斜率之和为直线
的斜率之和为直线![]() 斜率的
斜率的![]() 倍?若存在,求出定点
倍?若存在,求出定点![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
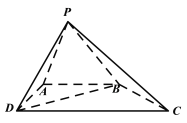
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动直线
中,动直线![]() 交抛物线
交抛物线![]() 于A,B两点.
于A,B两点.
(1)若![]() ,证明直线
,证明直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)点M为![]() 的中点,过点M作与y轴垂直的直线交抛物线
的中点,过点M作与y轴垂直的直线交抛物线![]() 于C点;点N为
于C点;点N为![]() 的中点,过点N作与y轴垂直的直线交抛物线
的中点,过点N作与y轴垂直的直线交抛物线![]() 于点P.设△
于点P.设△![]() 的面积
的面积![]() ,△
,△![]() 的面积为
的面积为![]() .
.
(i)若![]() 过定点
过定点![]() ,求使
,求使![]() 取最小值时,直线
取最小值时,直线![]() 的方程;
的方程;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,E为线段PB的中点,F为线段BC上的动点.

(1)求证:AE⊥平面PBC;
(2)试确定点F的位置,使平面AEF与平面PCD所成的锐二面角为30°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的左,右焦点
的左,右焦点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得
,使得![]() 的面积与
的面积与![]() (
(![]() 为原点)的面积相等?若存在,求出
为原点)的面积相等?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com