
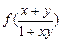 ; ②当x∈(-1,0),f (x) > 0.
; ②当x∈(-1,0),f (x) > 0. 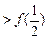 .
.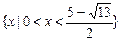
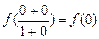 ∴ f (0) = 0
∴ f (0) = 0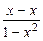 ) = f (0) = 0
) = f (0) = 0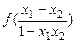
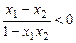 ∴
∴ 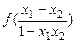 > 0
> 0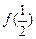

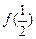 …………………8分
…………………8分 为
为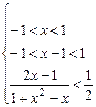
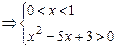
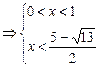 或
或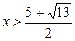
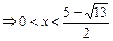
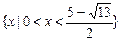 …………………12分
…………………12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
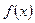 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(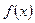 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),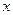 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式:
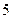 分钟与开讲
分钟与开讲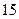 分钟比较,学生的接受能力何时强一些?
分钟比较,学生的接受能力何时强一些?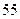 的接受能力以及
的接受能力以及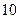 分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com