
(本小题共12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
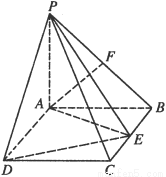
(1)当点E为BC的中点时, 证明EF//平面PAC;
(2)求三棱锥E-PAD的体积;
(3)证明:无论点E在边BC的何处,都有PE AF.
AF.
(1)见解析;(2) (3)见解析.
(3)见解析.
【解析】
试题分析:(1)利用线面平行的判断定理证明线面平行归根结底是证明线线平行,关键是要注意一条直线在平面内另一条直线在平面外.(2)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.(3)证明线线垂直的方法较多,如证明线面垂直、勾股定理、余弦定理.(4)另外解题时,注意线线、线面与面面关系的相互转化.
试题解析:(1)证明: 连结AC,EF
∵点E、F分别是边BC、PB的中点
∴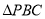 中,
中,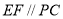 2分
2分
又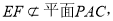
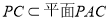 3分
3分
∴当点E是BC的中点时,EF//平面PAC 4分
(2)∵PA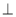 平面ABCD且
平面ABCD且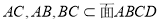
∴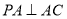 ,
,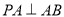 ,
,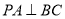
∴ 中,PA =
中,PA =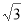 ,AD=1
,AD=1
∴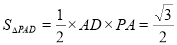 6分
6分
又四边形ABCD为矩形
∴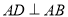
又AD和PA是面PAD上两相交直线
∴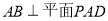
又AD//BC
∴AB就是三棱锥E-PAD的高. 7分
∴ . 8分
. 8分
(3)∵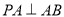 ,PA=AB=
,PA=AB=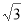 ,点F是PB的中点
,点F是PB的中点
∴等腰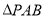 中,
中,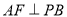 9分
9分
又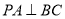 ,
,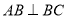 且PA和AB是平面PAB上两相交直线
且PA和AB是平面PAB上两相交直线
∴BC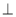 平面PAB
平面PAB
又
∴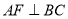 10分
10分
又PB和BC是平面PBC上两相交直线
∴ 11分
11分
又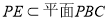 ∴
∴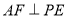
∴无论点E在边BC的何处,都有PE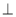 AF成立. 12分
AF成立. 12分
考点:空间几何体的线线、线面关系以及体积公式.


科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试理科数学试卷(解析版) 题型:解答题
如图,在四棱锥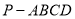 中,
中,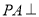 底面
底面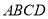 ,
,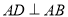 ,
,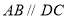 ,
, ,
,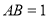 ,点
,点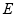 为棱
为棱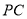 的中点.
的中点.
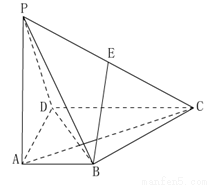
(Ⅰ)证明: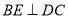 ;
;
(Ⅱ)求直线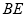 与平面
与平面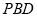 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省等五校高三上学期第二次联考文科数学试卷(解析版) 题型:选择题
设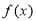 是定义在R上的周期为
是定义在R上的周期为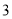 的函数,当x∈[-2,1)时,
的函数,当x∈[-2,1)时, ,则
,则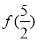 =
=
A.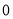 B.
B.  C.
C.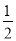 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省等五校高三上学期第二次联考理科数学试卷(解析版) 题型:选择题
在区间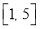 和
和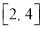 上分别取一个数,记为
上分别取一个数,记为 , 则方程
, 则方程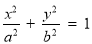 表示焦点在
表示焦点在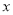 轴上且离心率小于
轴上且离心率小于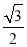 的椭圆的概率为 ( )
的椭圆的概率为 ( )
A. B.
B.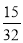 C.
C. D.
D.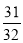
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一上学期期中考试文科数学试卷(解析版) 题型:选择题
已知直线 与圆
与圆 交于
交于 、
、 两点,若
两点,若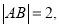 则实数
则实数 的值为( )
的值为( )
A. B.
B. C.
C.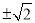 D.
D.
A.3 B.2 C.1 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com