
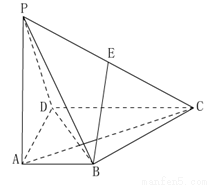
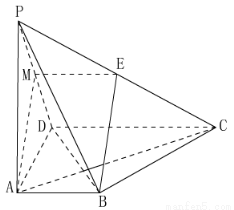
如图,在四棱锥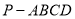 中,
中,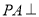 底面
底面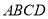 ,
,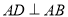 ,
,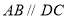 ,
, ,
,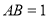 ,点
,点 为棱
为棱 的中点.
的中点.
(Ⅰ)证明: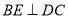 ;
;
(Ⅱ)求直线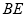 与平面
与平面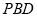 所成角的正切值.
所成角的正切值.
(Ⅰ)详见解析;(Ⅱ)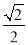
【解析】
试题分析:(1)取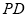 中点
中点 ,连接
,连接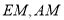 .证四边形
.证四边形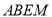 为平行四边形可得
为平行四边形可得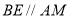 .通过证
.通过证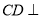 平面
平面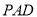 ,可得
,可得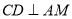 ,又
,又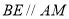 ,所以
,所以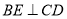 ;
;
(2)由(1)及已知可证平面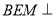 平面
平面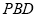 ,所以可得直线
,所以可得直线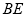 在平面
在平面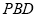 内的射影必为
内的射影必为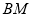 ,解三角形可得
,解三角形可得 与平面
与平面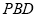 所成的角的正切值为
所成的角的正切值为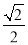 。
。
试题解析:(1)如图,取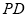 中点
中点 ,连接
,连接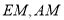 .
.
由于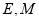 分别为
分别为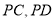 的中点, 故
的中点, 故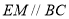 ,且
,且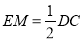 ,又由已知,可得
,又由已知,可得 且
且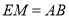 ,故四边形
,故四边形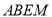 为平行四边形,所以
为平行四边形,所以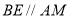 .
.
因为 底面
底面 ,故
,故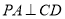 ,而
,而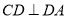 ,从而
,从而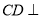 平面
平面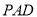 ,因为
,因为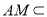 平面
平面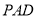 ,于是
,于是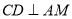 ,又
,又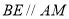 ,所以
,所以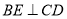 .
.
(2)连接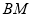 ,由(Ⅰ)有
,由(Ⅰ)有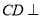 平面
平面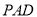 ,得
,得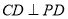 ,
,
而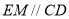 ,故
,故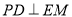 .
.
又因为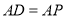 ,
,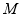 为
为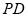 的中点,故
的中点,故 ,从而
,从而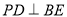 ,所以
,所以 平面
平面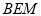 ,
,
故平面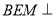 平面
平面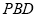 .
.
所以直线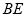 在平面
在平面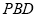 内的射影为直线
内的射影为直线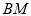 ,
,
而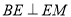 ,可得
,可得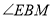 为锐角,
为锐角,
故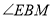 为直线
为直线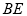 与平面
与平面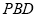 所成的角.
所成的角.
依题意,有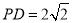 ,而
,而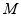 为
为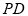 中点,可得
中点,可得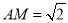 ,进而
,进而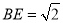 .
.
故在直角三角形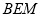 中,
中,
所以直线 与平面
与平面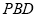 所成的角的正切值为
所成的角的正切值为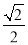
考点:线线、线面、面面平行、垂直的判定与性质,求线面角。


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:2014-2015学年山东省日照市高三12月校际联合检测理科数学试卷(解析版) 题型:选择题
已知实数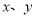 满足约束条件
满足约束条件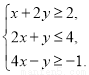 若
若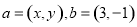 ,设
,设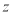 表示向量
表示向量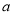 在向量
在向量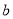 方向上射影的数量,则z的取值范围是( )
方向上射影的数量,则z的取值范围是( )
A.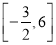 B.
B.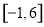 C.
C.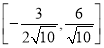 D.
D.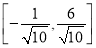
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
在△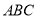 中,角
中,角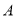 ,
,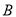 ,
,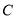 所对的边分别为
所对的边分别为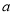 ,
,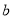 ,
,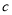 ,若
,若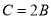 ,则
,则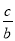 为( )
为( )
A. B.
B.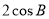 C.
C.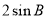 D.
D.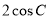
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题共12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
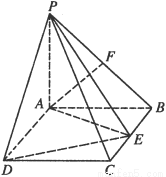
(1)当点E为BC的中点时, 证明EF//平面PAC;
(2)求三棱锥E-PAD的体积;
(3)证明:无论点E在边BC的何处,都有PE AF.
AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com