
已知过抛物线y2=2px(p>0)的焦点的直线交抛物线于A、B两点,且AB=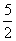 p,求AB所在的直线方程.
p,求AB所在的直线方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
对于曲线C: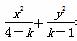 =1,给出下面四个命题:
=1,给出下面四个命题:
①曲线C不可能表示椭圆;
②当1<k<4时,曲线C表示椭圆;
③若曲线C表示双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<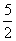 .
.
其中所有正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比,与它的长度 的平方成反比.
的平方成反比.
(Ⅰ)在a>d>0的条件下,将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷会发生变化吗?变大还是变小?
(Ⅱ)现有一根横截面为半圆(半圆的半径为R= )的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
)的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com