
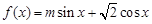 ,
,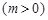 的最大值为2.
的最大值为2.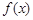 在
在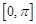 上的值域;
上的值域;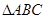 外接圆半径
外接圆半径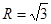 ,
,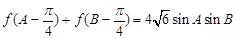 ,角
,角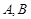 所对的边分别是
所对的边分别是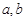 ,求
,求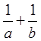 的值.
的值. 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:不详 题型:解答题
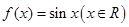 与
与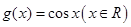 .
.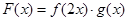 ,有下列结论:①
,有下列结论:①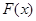 是奇函数;②
是奇函数;②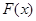 是周期函数,最小正周期为
是周期函数,最小正周期为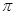 ;③
;③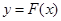 的图象关于点
的图象关于点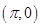 对称;④
对称;④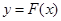 的图象关于直线
的图象关于直线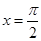 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)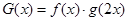 ,求满足
,求满足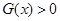 的
的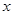 的取值范围;
的取值范围;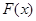 的值域为
的值域为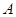 ,函数
,函数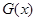 的值域为
的值域为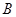 ,试判断集合
,试判断集合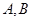 之间的关系.
之间的关系.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
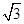 sin2x+2cos2x+m在区间[0,
sin2x+2cos2x+m在区间[0,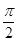 ]上的最大值为3,则
]上的最大值为3,则查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
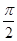 )的部分图象如图所示,则( )
)的部分图象如图所示,则( )
A.ω=2,φ= | B.ω=1,φ=- |
C.ω=1,φ= | D.ω=2,φ=- |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com