
已知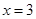 是函数
是函数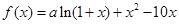 的一个极值点。
的一个极值点。
(Ⅰ)求 ;
;
(Ⅱ)求函数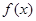 的单调区间;
的单调区间;
(Ⅲ)若直线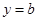 与函数
与函数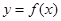 的图象有3个交点,求
的图象有3个交点,求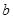 的取值范围。
的取值范围。
(Ⅰ)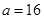 ;(Ⅱ)单调增区间是
;(Ⅱ)单调增区间是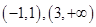 ,单调减区间是
,单调减区间是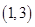 ;
;
(Ⅲ)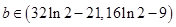
解析试题分析:(Ⅰ)因为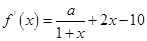 ,
,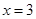 是函数
是函数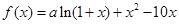 的一个极值点,所以
的一个极值点,所以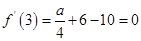 ,
,
因此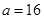 . ---3分
. ---3分
(Ⅱ)由(Ⅰ)知,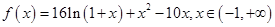
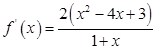 ,
,
当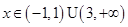 时,
时,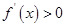
当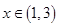 时,
时,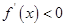
所以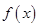 的单调增区间是
的单调增区间是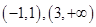 , ---6分
, ---6分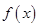 的单调减区间是
的单调减区间是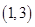 . ---8分
. ---8分
(Ⅲ)由(Ⅱ)知,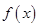 在
在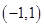 内单调增加,在
内单调增加,在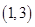 内单调减少,在
内单调减少,在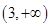 上单调增加,
上单调增加,
且当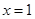 或
或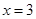 时,
时,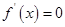
所以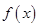 的极大值为
的极大值为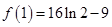 ,极小值为
,极小值为 . ---10分
. ---10分
因此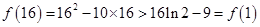
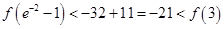
所以在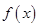 的三个单调区间
的三个单调区间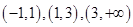 ,
,
因为直线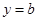 有
有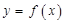 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当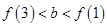
因此,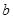 的取值范围为
的取值范围为 . ---12分
. ---12分
考点:本小题主要考查函数、导函数等基础知识,运用导函数研究函数性质(单调性、最值),以及利用函数的单调性考查已知两函数交点各数时参数的取值范围,考查学生代数恒等变形能力和综合运用数学知识分析问题和解决问题的能力.
点评:导数的工具性使得导数在高考中的应用有得天独厚的优势,特别是在研究函数的性质方面.近年,各地高考都从不同的方面对导数内容进行考查,既有考查导数的小题,又有考查导数综合应用的大题.


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数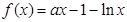
 .
.
(Ⅰ)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数 在
在 处取得极值,对
处取得极值,对
 ,
, 恒成立,
恒成立,
求实数 的取值范围;
的取值范围;
(Ⅲ)当 且
且 时,试比较
时,试比较 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com