
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为 2 的正三角形,顶点
是边长为 2 的正三角形,顶点 ![]() 在底面
在底面![]() 上的射影为
上的射影为![]() 的中心,若
的中心,若![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,则三棱锥
,则三棱锥![]() 外接球的表面积为( )
外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,底面ABCD四边长为1的菱形,∠ABC=![]() ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
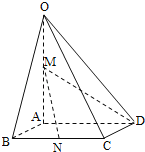
(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小;
(3)求点B到平面OCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
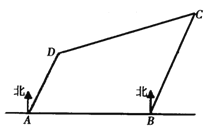
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为![]() 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是![]() .
.
(1)若椭圆C上一动点![]() 满足
满足![]() ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点![]() 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为![]() ,求P点的坐标;
,求P点的坐标;
(3)已知![]() ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点![]() 的直线的最短距离
的直线的最短距离![]() .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的为( )
A. 由金、银、铜、铁可导电,猜想:金属都可导电
B. 猜想数列![]() 的通项公式为
的通项公式为![]()
C. 半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]()
D. 由平面直角坐标系中圆的方程为![]() ,推测空间直角坐标系中球的方程为
,推测空间直角坐标系中球的方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于任意![]() ,满足条件
,满足条件![]() 且
且![]() 是与
是与![]() 无关的常数
无关的常数![]() 的无穷数列
的无穷数列![]() 称为
称为![]() 数列.
数列.
(1)若![]() ,证明:数列
,证明:数列![]() 是
是![]() 数列;
数列;
(2)设数列![]() 的通项为
的通项为![]() ,且数列
,且数列![]() 是
是![]() 数列,求常数
数列,求常数![]() 的取值范围;
的取值范围;
(3)设数列![]() ,问数列
,问数列![]() 是否是
是否是![]() 数列?请说明理由.
数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经济订货批量模型,是目前大多数工厂、企业等最常采用的订货方式,即某种物资在单位时间的需求量为某常数,经过某段时间后,存储量消耗下降到零,此时开始订货并随即到货,然后开始下一个存储周期,该模型适用于整批间隔进货、不允许缺货的存储问题,具体如下:年存储成本费![]() (元)关于每次订货
(元)关于每次订货![]() (单位)的函数关系
(单位)的函数关系![]() ,其中
,其中![]() 为年需求量,
为年需求量,![]() 为每单位物资的年存储费,
为每单位物资的年存储费,![]() 为每次订货费. 某化工厂需用甲醇作为原料,年需求量为6000吨,每吨存储费为120元/年,每次订货费为2500元.
为每次订货费. 某化工厂需用甲醇作为原料,年需求量为6000吨,每吨存储费为120元/年,每次订货费为2500元.
(1)若该化工厂每次订购300吨甲醇,求年存储成本费;
(2)每次需订购多少吨甲醇,可使该化工厂年存储成本费最少?最少费用为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“90后”指1990年及以后出生,“80后”指1980-1989年之间出生,“80前”指1979年及以前出生.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )

A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com