
分析 设直线l的方程为x=ty+3,代入抛物线方程,由韦达定理求得$\overrightarrow{OA}⊥\overrightarrow{OB}$,则∠AOB=90°.
解答 解:依题意知直线l斜率不为0,则可设直线l的方程为x=ty+3,
代入y2=3x,得y2-3ty-9=0.
设A(x1,y1),B(x2,y2),则y1+y2=3t,y1y2=-9.
$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y1,
=(ty1+3)(ty2+3)+y1y1,
=(1+t2)y1y1+3t(y1+y2)+9,
=(1+t2)(-9)+3t×3t+9,
=0
所以$\overrightarrow{OA}⊥\overrightarrow{OB}$,即∠AOB=90°.
故答案为:90°.
点评 本题考查抛物线的简单几何性质,直线与抛物线的位置关系,考查向量数量积的坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.| 非手机迷 | 手机迷 | 合计 | |
| 男 | x | x | m |
| 女 | y | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(k2≥x0) | 0.05 | 0.10 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD中,平面PCD⊥平面ABCD,且PD=PC=$\frac{\sqrt{2}}{2}$CD=$\frac{\sqrt{2}}{2}$BC,∠BCD=$\frac{2π}{3}$,△ABD是等边三角形,AC∩BD=E.
已知四棱锥P-ABCD中,平面PCD⊥平面ABCD,且PD=PC=$\frac{\sqrt{2}}{2}$CD=$\frac{\sqrt{2}}{2}$BC,∠BCD=$\frac{2π}{3}$,△ABD是等边三角形,AC∩BD=E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
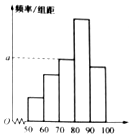 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com