
【题目】如图,已知直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() .
.
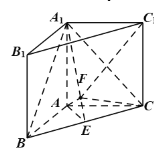
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
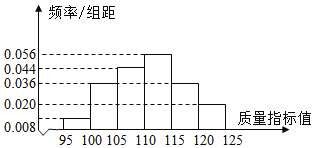
(1)根据表1和图1,通过计算合格率对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: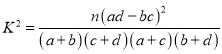 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围;
的取值范围;
(3)证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥A-BCDE,其中AC=BC=2,AC⊥BC,CD//BE且CD=2BE,CD⊥平面ABC,F为AD的中点.
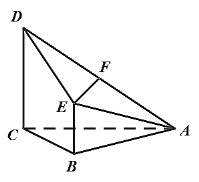
(1)求证:EF//平面ABC;
(2)设M是AB的中点,若DM与平面ABC所成角的正切值为![]() ,求平面ACD与平面ADE夹角的余弦值.
,求平面ACD与平面ADE夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a﹣1)x+y+a+3=0,(a∈R).
(1)若直线l在两坐标轴上截距的绝对值相等,求直线l的方程;
(2)若直线l不经过第一象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]()
![]() (
(![]() )的半焦距为
)的半焦距为![]() ,原点
,原点![]() 到经过两点
到经过两点![]() ,
,![]() 的直线的距离为
的直线的距离为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)如图,![]() 是圆
是圆![]()
![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点A(0,﹣1),B(0,1),直线PA,PB相交于点P,且它们的斜率之积是![]() ,记点P轨迹为C.
,记点P轨迹为C.
(1)求曲线C的轨迹方程;
(2)直线l与曲线C交于M,N两点,若|AM|=|AN|,求直线l的斜率k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com