
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,则称
…,则称![]() 是
是![]() 的“收缩数列”.其中,
的“收缩数列”.其中,![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
【答案】(1)![]() (2)证明见解析(3)所有满足该条件的数列
(2)证明见解析(3)所有满足该条件的数列![]() 为
为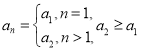
【解析】
(1)由![]() 可得
可得![]() 为递增数列,
为递增数列,![]() ,
,![]() ,从而易得
,从而易得![]() ;
;
(2)利用![]() ,
,
![]() ,可证
,可证![]() 是不减数列(即
是不减数列(即![]() ),而
),而![]() ,由此可得
,由此可得![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() .
.
(3)首先,由已知,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() (*),这里分析
(*),这里分析![]() 与
与![]() 的大小关系,
的大小关系,![]() ,
,![]() 均出现矛盾,
均出现矛盾,![]() ,结合(*)式可得
,结合(*)式可得![]() ,因此猜想
,因此猜想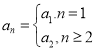 (
(![]() ),用反证法证明此结论成立,证明时假设
),用反证法证明此结论成立,证明时假设![]() 是首次不符合
是首次不符合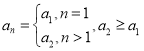 的项,则
的项,则![]() ,这样题设条件变为
,这样题设条件变为![]() (*),仿照讨论
(*),仿照讨论![]() 的情况讨论
的情况讨论![]() ,可证明.
,可证明.
解:(1)由![]() 可得
可得![]() 为递增数列,
为递增数列,
所以![]() ,
,
故![]() 的前
的前![]() 项和为
项和为![]() .
.
(2)因为![]() ,
,
![]() ,
,
所以![]()
所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() .
.
(3)由![]() 可得
可得
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() (*),
(*),
若![]() ,则
,则![]() ,所以由(*)可得
,所以由(*)可得![]() ,与
,与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,所以由(*)可得
,所以由(*)可得![]() ,
,
所以![]() 与
与![]() 同号,这与
同号,这与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,由(*)可得
,由(*)可得![]() .
.
猜想:满足![]() 的数列
的数列![]() 是:
是:
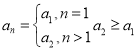 .
.
经验证,左式![]() ,
,
右式![]() .
.
下面证明其它数列都不满足(3)的题设条件.
法1:由上述![]() 时的情况可知,
时的情况可知,![]() 时,
时,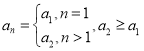 是成立的.
是成立的.
假设![]() 是首次不符合
是首次不符合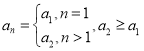 的项,则
的项,则![]() ,
,
由题设条件可得![]() (*),
(*),
若![]() ,则由(*)式化简可得
,则由(*)式化简可得![]() 与
与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,所以由(*)可得
,所以由(*)可得![]()
所以![]() 与
与![]() 同号,这与
同号,这与![]() 矛盾;
矛盾;
所以![]() ,则
,则![]() ,所以由(*)化简可得
,所以由(*)化简可得![]() .
.
这与假设![]() 矛盾.
矛盾.
所以不存在数列不满足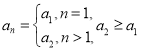 的
的![]() 符合题设条件.
符合题设条件.
法2:当![]() 时,
时,![]() ,
,
所以![]()
即![]()
由![]() 可得
可得![]()
又![]() ,所以可得
,所以可得![]() ,
,
所以![]() ,
,
即![]()
所以![]() 等号成立的条件是
等号成立的条件是
![]() ,
,
所以,所有满足该条件的数列![]() 为
为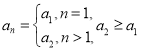 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,如果存在常数
上的函数,如果存在常数![]() ,对区间
,对区间![]() 的任意划分:
的任意划分:![]() ,和式
,和式![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 上的“绝对差有界函数”。注:
上的“绝对差有界函数”。注:![]() 。
。
(1)证明函数![]() 在
在![]() 上是“绝对差有界函数”。
上是“绝对差有界函数”。
(2)证明函数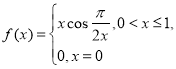 不是
不是![]() 上的“绝对差有界函数”。
上的“绝对差有界函数”。
(3)记集合![]() 存在常数
存在常数![]() ,对任意的
,对任意的![]() ,有
,有![]() 成立
成立![]() ,证明集合
,证明集合![]() 中的任意函数
中的任意函数![]() 为“绝对差有界函数”,并判断
为“绝对差有界函数”,并判断![]() 是否在集合
是否在集合![]() 中,如果在,请证明并求
中,如果在,请证明并求![]() 的最小值;如果不在,请说明理由。
的最小值;如果不在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某甲![]() 篮球队的12名队员(含2名外援)中有5名主力队员(含一名外援),主教练要从12名队员中选5人首发上场,则主力队员不少于4人,且有一名外援上场的概率是_____.
篮球队的12名队员(含2名外援)中有5名主力队员(含一名外援),主教练要从12名队员中选5人首发上场,则主力队员不少于4人,且有一名外援上场的概率是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 和函数
和函数![]() ,
,
(1)若![]() 为偶函数,试判断
为偶函数,试判断![]() 的奇偶性;
的奇偶性;
(2)若方程![]() 有两个不等的实根
有两个不等的实根![]() ,则
,则
①试判断函数![]() 在区间
在区间![]() 上是否具有单调性,并说明理由;
上是否具有单调性,并说明理由;
②若方程![]() 的两实根为
的两实根为![]() 求使
求使![]() 成立的
成立的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在一条景观道的一端有一个半径为![]() 米的圆形摩天轮O,逆时针
米的圆形摩天轮O,逆时针![]() 分钟转一圈,从
分钟转一圈,从![]() 处进入摩天轮的座舱,
处进入摩天轮的座舱,![]() 垂直于地面
垂直于地面![]() ,在距离
,在距离![]() 处
处![]() 米处设置了一个望远镜
米处设置了一个望远镜![]() .
.

(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱![]() 分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜
分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜![]() 中仔细观看.问望远镜
中仔细观看.问望远镜![]() 的仰角
的仰角![]() 应调整为多少度?(精确到1度)
应调整为多少度?(精确到1度)
(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带![]() ,发现取景的视角
,发现取景的视角![]() 恰为
恰为![]() ,求绿化带
,求绿化带![]() 的长度(精确到1米)
的长度(精确到1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行,第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事,也是继北京奥运会之后我国举办的规模最大的国际体育盛会.来自109个国家的9300余名军体健儿在江城武汉同场竞技、增进友谊.运动会共设置射击、游泳、田径、篮球等27个大项、329个小项.经过激烈角逐,奖牌榜的前6名如下:
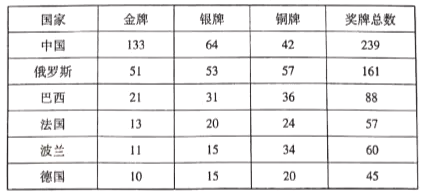
某大学德语系同学利用分层抽样的方式从德国获奖选手中抽取了9名获奖代表.
(1)请问这9名获奖代表中获金牌、银牌、铜牌的人数分别是多少人?
(2)从这9人中随机抽取3人,记这3人中银牌选手的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)从这9人中随机抽取3人,求已知这3人中有获金牌运动员的前提下,这3人中恰好有1人为获铜牌运动员的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在争创文明城市过程中,为调查市民对文明出行机动车礼让行人的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于45岁 | 80 | ||
年龄大于45岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄段与是否支持文明出行机动车礼让行人有关?
(3)已知在被调查的年龄小于25岁的支持者有5人,其中2人是教师,现从这5人中随机抽取3人,求至多抽到1位教师的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com