已知数列{an}的前n项和为Sn,且a1=1,an+1=2Sn.
(1)求a2,a3,a4的值;
(2)求数列{an}的通项公式an;
(3)设bn=nan,求数列{bn}的前n项和Tn.
解:(1)∵a
1=1,
∴a
2=2a
1=2,a
3=2S
2=6,a
4=2S
3=18,
(2)∵a
n+1=2S
1,∴a
N=2S
n-1(n≥2),
∴a
n+1-a
n=2a
n,
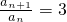
(n≥2)
又
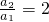
,∴数列{a
n}自第2项起是公比为3的等比数列,
∴
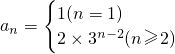
,
(3)∵b
n=na
n,∴
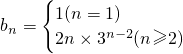
,
∴T
n=1+2×2×3
0+2×3×3
1+2×4×3
2++2×n×3
n-2,①
3T
n=3+2×2×3
1+2×3×3
2+2×4×3
3++2×n×3
n-1②(12分)
①-②得-2T
n=-2+2×2×3
0+2×3
1+2×3
2++2×3
n-2-2×n×3
n-1
=2+2(3+3
2+3
3++3
n-2)-2n×3
n-1=(1-2n)×3
n-1-1
∴
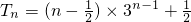
.(14分)
分析:(1)由a
1=1,a
n+1=2s
n,分别令n=1,2,3求出a
2,a
3,a
4的值;
(2)由a
n+1=2s
n及
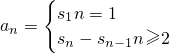
求得a
n,
(3)把(2)求得a
n代入中b
n,应用错位相减法求和.
点评:由数列前n 项和求数列通项公式时,一定注意n=1的情况,体现了分类讨论的数学思想;属中档题.

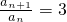 (n≥2)
(n≥2)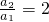 ,∴数列{an}自第2项起是公比为3的等比数列,
,∴数列{an}自第2项起是公比为3的等比数列,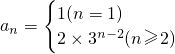 ,
,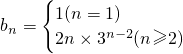 ,
,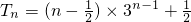 .(14分)
.(14分)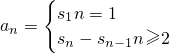 求得an,
求得an,

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案