
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() ,
,![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)定义:曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .若抛物线
.若抛物线![]() 上存在点
上存在点![]() (不与原点重合)处的切线交椭圆于
(不与原点重合)处的切线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .直线
.直线![]() 与过点
与过点![]() 且平行于
且平行于![]() 轴的直线的交点为
轴的直线的交点为![]() ,证明:点
,证明:点![]() 必在定直线上.
必在定直线上.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由![]() 得出
得出![]() ,再由
,再由![]() 得出
得出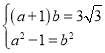 ,求出
,求出![]() 、
、![]() 的值,从而得出椭圆的标准方程;
的值,从而得出椭圆的标准方程;
(2)设点的坐标为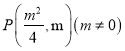 ,根据中定义得出直线
,根据中定义得出直线![]() 的方程,并设点
的方程,并设点![]() 、
、![]() ,
,![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,列出韦达定理,利用中点坐标公式求出点
的方程与椭圆的方程联立,列出韦达定理,利用中点坐标公式求出点![]() 的坐标,得出直线
的坐标,得出直线![]() 的方程与
的方程与![]() 的方程
的方程![]() 联立,求出点
联立,求出点![]() 的坐标,可得出点
的坐标,可得出点![]() 所在的定直线的方程.
所在的定直线的方程.
(1)由![]() ,可知
,可知![]() ,即
,即![]() .
.
![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,联立
,联立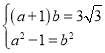 .
.
得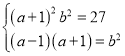 ,则
,则![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)设点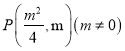 ,则由定义可知,过抛物线
,则由定义可知,过抛物线![]() 上任一点
上任一点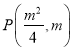 处的切线方程为
处的切线方程为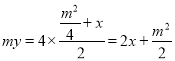 ,所以
,所以![]() .
.
设![]() 、
、![]() ,
,![]() .
.
联立方程组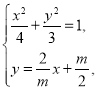 ,消去
,消去![]() ,得
,得![]() .
.
由![]() ,得
,得![]() ,解得
,解得![]() .
.
因为![]() ,
,
所以![]() ,从而
,从而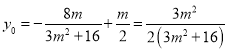 ,
,
所以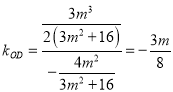 ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
而过点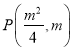 且平行于
且平行于![]() 轴的直线方程为
轴的直线方程为![]() ,
,
联立方程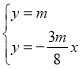 ,解得
,解得![]() ,所以点
,所以点![]() 在定直线上
在定直线上![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 分别是棱
分别是棱![]() 上的点,平面
上的点,平面![]() 平面
平面![]()
(Ⅰ)确定点![]() 的位置,并说明理由;
的位置,并说明理由;
(Ⅱ)求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 若满足:①对任意
若满足:①对任意![]() 、
、![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“中心捺函数”,其中点
为“中心捺函数”,其中点![]() 称为函数
称为函数![]() 的中心.已知函数
的中心.已知函数![]() 是以
是以![]() 为中心的“中心捺函数”,若满足不等式
为中心的“中心捺函数”,若满足不等式![]() ,当
,当![]() 时,
时,![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有200人参加了一次会议,为了了解这200人参加会议的体会,将这200人随机号为001,002,003,…,200,用系统抽样的方法(等距离)抽出20人,若编号为006,036,041,176, 196的5个人中有1个没有抽到,则这个编号是( )
A. 006B. 041C. 176D. 196
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元,假设甲机床某天生产50件零件,请估计甲机床该天的利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com