
【题目】已知函数![]() ,且曲线
,且曲线![]() 在
在![]() 处的切线与
处的切线与![]() 平行.
平行.
(1)求![]() 的值;
的值;
(2)当![]() 时,试探究函数
时,试探究函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析: (1)根据曲线![]() 在
在![]() 处的切线与
处的切线与![]() 平行可得:
平行可得: ![]() ,进而求出a值; (2)①当
,进而求出a值; (2)①当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 单调递增,根据零点存在性定理可得:
单调递增,根据零点存在性定理可得: ![]() 在
在![]() 上只有一个零点.②当
上只有一个零点.②当![]() 时,
时, ![]() 恒成立,构造函数
恒成立,构造函数![]() ,求导判断单调性与最值可得
,求导判断单调性与最值可得![]() ,
,
又![]() 时,
时, ![]() ,所以
,所以![]() ,即
,即![]() ,故函数
,故函数![]() 在
在![]() 上没有零点,③当
上没有零点,③当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递减,根据零点存在性定理可得:函数
上单调递减,根据零点存在性定理可得:函数![]() 在
在![]() 上有且只有一个零点,综上所述
上有且只有一个零点,综上所述![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
试题解析:解:(1)依题意![]() ,故
,故![]() ,
,
故![]() ,解得
,解得![]() .
.
(2)①当![]() 时,
时, ![]() ,此时
,此时![]() ,
, ![]() ,
,
函数![]() 在
在![]() 单调递增,
单调递增,
故函数![]() 在
在![]() 至多有一个零点,又
至多有一个零点,又![]() ,
,
而且函数![]() 在
在![]() 上是连续不断的,因此函数
上是连续不断的,因此函数![]() 在
在![]() 上只有一个零点.
上只有一个零点.
②当![]() 时,
时, ![]() 恒成立,证明如下:
恒成立,证明如下:
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 时,
时, ![]() ,所以
,所以![]() ,
,
又![]() 时,
时, ![]() ,所以
,所以![]() ,即
,即![]() ,
,
故函数![]() 在
在![]() 上没有零点,
上没有零点,
③当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递减,故函数
上单调递减,故函数![]() 在
在![]() 至多有一个零点,
至多有一个零点,
又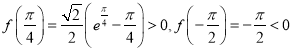 ,而且函数
,而且函数![]() 在
在![]() 上是连续不断的,
上是连续不断的,
因此,函数![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
综上所述![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|loga|x﹣1||(a>0,a≠1),若x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则 ![]() +
+ ![]() +
+ ![]() +
+ ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数.
上是增函数.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]()
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名学生组成一个样本,再从样本中抽出2名学生,记甲班被抽到的人数为ξ,求ξ的分布列和数学期望.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象经过点( ![]() ,
, ![]() ).
).
(1)求函数f(x)的解析式,并判断奇偶性;
(2)判断函数f(x)在(﹣∞,0)上的单调性,并用单调性定义证明.
(3)作出函数f(x)在定义域内的大致图象(不必写出作图过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题
①若“p或q”为假命题,则p,q均为真命题;
②命题“若x≥2且y≥3,则x+y≥5”的逆否命题为假命题;
③在△ABC中,“A>45°”是“sinA> ![]() ”的充要条件,
”的充要条件,
其中正确的命题个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com