[题目]在等比数列{}中..公比.且. 与的等比中项为2．(1)求数列{}的通项公式,(2)设 .求:数列{}的前项和为. 题目和参考答案——青夏教育精英家教网—

【题目】在等比数列｛｝中，，公比，且，与的等比中项为2．

（1）求数列｛｝的通项公式；

（2）设，求：数列｛｝的前项和为，

【答案】（1）（2）

【解析】

试题分析：（1）由a1a5=，a2a8=原式可化为+2a3a5+＝25，即a3＋a5＝5，又由a3a5＝4，解出q，a1即可.（2）代入中，得到bn＝5－n，即数列，{bn}是以4为首项，－1为公差的等差数列，根据等差数列的前n项和公式求之即可.

试题解析：解：（1）因为a1a5+2a3a5+a2a8＝25，所以，+2a3a5+＝25

又an＞o，…a3＋a5＝5， 3分

又a3与a5的等比中项为2，所以，a3a5＝4

而q（0,1），所以，a3＞a5，所以，a3＝4，a5＝1，，a1＝16，所以，

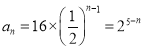6分

（2）bn＝log2an＝5－n，所以，bn＋1－bn＝－1，

所以，{bn}是以4为首项，－1为公差的等差数列 8分

所以， 10分

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数，且曲线在处的切线与平行.

（1）求的值；

（2）当时，试探究函数的零点个数，并说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某课题组对春晚参加“咻一咻”抢红包活动的同学进行调查，按照使用手机系统不同（安卓系统和IOS系统）分别随机抽取5名同学进行问卷调查，发现他们咻得红包总金额数如表所示：

手机系统	一	二	三	四	五
安卓系统（元）	2	5	3	20	9
IOS系统（元）	4	3	18	9	7

（1）如果认为“咻”得红包总金额超过6元为“咻得多”，否则为“咻得少”，请判断手机系统与咻得红包总金额的多少是否有关？
（2）要从5名使用安卓系统的同学中随机选出2名参加一项活动，以X表示选中的同学中咻得红包总金额超过6元的人数，求随机变量X的分布列及数学期望E（X）．
下面的临界值表供参考：

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

独立性检验统计量，其中n=a+b+c+d．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy中，直线l的参数方程为：（t为参数，其中0＜α＜），椭圆M的参数方程为（β为参数），圆C的标准方程为（x﹣1）2+y2=1．
（1）写出椭圆M的普通方程；
（2）若直线l为圆C的切线，且交椭圆M于A，B两点，求弦AB的长．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一种计算装置，有一数据入口A和一个运算出口B，按照某种运算程序：①当从A口输入自然数1时，从B口得到，记为；②当从A口输入自然数n（n≥2）时，在B口得到的结果f（n）是前一个结果f（n﹣1）的倍．（Ⅰ）当从A口分别输入自然数2，3，4时，从B口分别得到什么数？
（Ⅱ）根据（Ⅰ）试猜想f（n）的关系式，并用数学归纳法证明你的结论．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：
（i）对任意的x∈[0，1]，恒有f（x）≥0；
（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．
则下列四个函数中不是M函数的个数是（）
①f（x）=x2②f（x）=x2+1
③f（x）=ln（x2+1）④f（x）=2x﹣1．
A.1
B.2
C.3
D.4