
【题目】设函数f(x)= ![]() .
.
(1)当m=4时,求函数f(x)的定义域M;
(2)当a,b∈RM时,证明:2|a+b|<|4+ab|.
【答案】
(1)解:当m=4时,由|x+1|+|x﹣1|≥4,
等价于 ![]() 或
或 ![]() 或
或 ![]() ,
,
解得x≤﹣2或x≥2或x∈.
则不等式的解集为M={x|x≤﹣2或x≥2}
(2)解:证明:当a,b∈CRM时,即﹣2<a,b<2,
所以4(a+b)2﹣(4+ab)2=4(a2+2ab+b2)﹣(16+8ab+a2b2)
=4a2+4b2﹣16﹣a2b2=(a2﹣4)(4﹣b2)<0,所以4(a+b)2<(4+ab)2,
即2|a+b|<|4+ab|
【解析】(1)由题意和二次根式的被开方数非负,可得|x+1|+|x﹣1|≥4,运用绝对值的意义和对x讨论,解不等式即可得到所求定义域;(2)可得﹣2<a,b<2,要证2|a+b|<|4+ab|,可证4(a+b)2<(4+ab)2 , 作差4(a+b)2﹣(4+ab)2 , 运用平方差和因式分解,即可得证.
【考点精析】利用函数的定义域及其求法对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】下列命题中错误的个数为:( )
①![]() 的图像关于点
的图像关于点![]() 对称;②
对称;②![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③![]() 的图像关于直线
的图像关于直线![]() 对称;④
对称;④![]() 的图像关于直线
的图像关于直线![]() 对称。
对称。
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1+x)+lg(1﹣x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是100(5x+1﹣ ![]() )元.
)元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且此函数图象过点(1,5).
,且此函数图象过点(1,5).
(1)求实数m的值;
(2)判断f(x)奇偶性;
(3)讨论函数f(x)在[2,+∞)上的单调性?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某校高二同学是否需要学校提供学法指导,用简单随机抽样方法从该校高二年级调查了55位同学,结果如下:
男 | 女 | |
需要 | 20 | 10 |
不需要 | 10 | 15 |
(Ⅰ)估计该校高二年级同学中,需要学校提供学法指导的同学的比例(用百分数表示,保留两位有效数字);
(Ⅱ)能否有95%的把握认为该校高二年级同学是否需要学校提供学法指导与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查方法来估计该校高二年级同学中,需要学校提供学法指导?说明理由.
附:![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市在海岛A上建了一水产养殖中心.在海岸线l上有相距70公里的B、C两个小镇,并且AB=30公里,AC=80公里,已知B镇在养殖中心工作的员工有3百人,C镇在养殖中心工作的员工有5百人.现欲在BC之间建一个码头D,运送来自两镇的员工到养殖中心工作,又知水路运输与陆路运输每百人每公里运输成本之比为1:2. 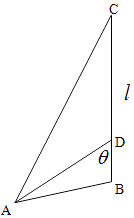
(1)求sin∠ABC的大小;
(2)设∠ADB=θ,试确定θ的大小,使得运输总成本最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com