
【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若![]() ,则
,则![]() ; ②若
; ②若![]() 则
则![]() ;③若
;③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着![]() 业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
(Ⅰ)完成下列列联表:
(Ⅱ)分析是否有![]() 的把握认为购买平板电脑与性别有关?
的把握认为购买平板电脑与性别有关?
附:独立性检验临界值表:

(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有大小相同的4个红球和2个白球,给出下列结论:
![]() 从中任取3球,恰有一个白球的概率是
从中任取3球,恰有一个白球的概率是![]() ;
;
![]() 从中有放回的取球6次,每次任取一球,则取到红球次数的方差为
从中有放回的取球6次,每次任取一球,则取到红球次数的方差为![]() ;
;
![]() 从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为![]() .
.
其中所有正确结论的序号是______ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(x+ ![]() ),则下列结论错误的是( )
),则下列结论错误的是( )
A.f(x)的一个周期为﹣2π
B.y=f(x)的图象关于直线x= ![]() 对称
对称
C.f(x+π)的一个零点为x= ![]()
D.f(x)在( ![]() ,π)单调递减
,π)单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10 ![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(Ⅱ)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.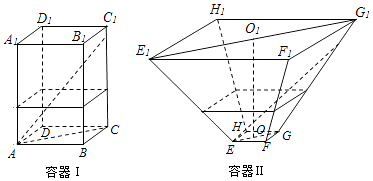
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com