
| A. | $\frac{1}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{9}$ |
分析 由已知利用两角和的正切函数公式即可计算得解.
解答 解:∵tan(α-β)=$\frac{2}{3}$,tan($\frac{π}{6}$-β)=$\frac{1}{2}$,
∴tan(α-$\frac{π}{6}$)=tan[(α-β)-($\frac{π}{6}$-β)]=$\frac{tan(α-β)-tan(\frac{π}{6}-β)}{1+tan(α-β)tan(\frac{π}{6}-β)}$=$\frac{\frac{2}{3}-\frac{1}{2}}{1+\frac{2}{3}×\frac{1}{2}}$=$\frac{1}{8}$.
故选:C.
点评 本题主要考查了两角和的正切函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:解答题
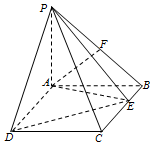 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
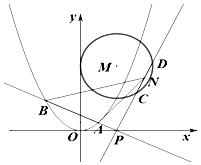 如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:填空题
某学校有教师300人,其中高级教师90人,中级教师150人,初级教师60人,为了了解教师健康状况,从中抽取40人进行体检.用分层抽样方法抽取高级、中级、初级教师人数分别为_______、________、_________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com