
【题目】在平面直角坐标系xOy内,点(![]() )在椭圆E:
)在椭圆E:![]() (a>0,b>0),椭圆E的离心率为
(a>0,b>0),椭圆E的离心率为![]() ,直线l过左焦点F且与椭圆E交于A、B两点
,直线l过左焦点F且与椭圆E交于A、B两点
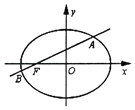
(1)求椭圆E的标准方程;
(2)若动直线l与x轴不重合,在x轴上是否存在定点P,使得PF始终平分∠APB?若存在,请求出点P的坐标:若不存在,请说明理由.
【答案】(1)![]() 1;(2)存在,P(﹣4,0)
1;(2)存在,P(﹣4,0)
【解析】
(1)根据![]() ,a2=b2+c2和点(
,a2=b2+c2和点(![]() )在椭圆E上,可得;(2)假设存在定点P(t,0)满足题意,设直线l的方程x=my﹣2,A(x,y),B(x',y'),
)在椭圆E上,可得;(2)假设存在定点P(t,0)满足题意,设直线l的方程x=my﹣2,A(x,y),B(x',y'),
(1)由题意得:e![]() ,a
,a![]() ,
,![]() 1,且a2=b2+c2,解得:a2=8,b2=4,
1,且a2=b2+c2,解得:a2=8,b2=4,
所以椭圆E的方程:![]() 1;
1;
(2)假设存在定点P(t,0)满足题意,由(1)得左焦点F(﹣2,0),
设直线l的方程:x=my﹣2,A(x,y),B(x',y'),
联立与椭圆的方程整理得:(2+m2)y2﹣4my﹣4=0,
∴y+y'![]() ,yy'
,yy'![]() ,
,
PF始终平分∠APB知:kAP+kBP=0,
所以kAP+kBP![]() 0,
0,
又x=my﹣2,x'=my'﹣2,
∴2myy'﹣(t+2)(y+y')=0,
即2m![]() (t+2)
(t+2)![]() 0,
0,
即(t+4)m=0,
∴t=﹣4,
所以存在定点P(﹣4,0)满足题意


科目:高中数学 来源: 题型:
【题目】为了调查民众对国家实行“新农村建设”政策的态度,现通过网络问卷随机调查了年龄在20周岁至80周岁的100人,他们年龄频数分布和支持“新农村建设”人数如下表:
年龄 |
|
|
|
|
|
|
频数 | 10 | 20 | 30 | 20 | 10 | 10 |
支持“新农村建设” | 3 | 11 | 26 | 12 | 6 | 2 |
(1)根据上述统计数据填下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(2)为了进一步推动“新农村建设”政策的实施,中央电视台某节目对此进行了专题报道,并在节目最后利用随机拨号的形式在全国范围内选出4名幸运观众(假设年龄均在20周岁至80周岁内),给予适当的奖励.若以频率估计概率,记选出4名幸运观众中支持“新农村建设”人数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时 ①求f0(x)和fk(x)的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
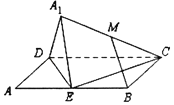
【题目】如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻折成△![]() DE,使平面
DE,使平面![]() DE⊥平面BCDE,若M为线段
DE⊥平面BCDE,若M为线段![]() C的中点,下面四个命题中不正确的是( )
C的中点,下面四个命题中不正确的是( )
A.BM![]() 平面
平面![]() DEB.CE⊥平面
DEB.CE⊥平面![]() DE
DE
C.DE![]() BMD.平面
BMD.平面![]() CD⊥平面
CD⊥平面![]() CE
CE
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有3名同学报名参加学校组织的辩论赛,现有甲、乙两个辨题可以选择,学校决定让选手以抽取卡片(除上面标的数不同外其他完全相同)的方式选择辩题,且每名选手抽取后放回.已知共有10张卡片,卡片上分别标有![]() 共10个数.若抽到卡片上的数为质数(2,3,5,7),则选择甲辨题,否则选择乙辩题.
共10个数.若抽到卡片上的数为质数(2,3,5,7),则选择甲辨题,否则选择乙辩题.
(1)求这3名同学中至少有1人选择甲辨题的概率.
(2)用X、Y分别表示这3名同学中选择甲、乙辨题的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆方程![]() (
(![]() ),
),![]() ,
,![]() 是椭圆的左右焦点,以
是椭圆的左右焦点,以![]() ,
,![]() 及椭圆短轴的一个端点为顶点的三角形是面积为
及椭圆短轴的一个端点为顶点的三角形是面积为![]() 的正三角形.
的正三角形.
(1)求椭圆方程;
(2)过![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() ,设
,设![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() 千米,汽车从
千米,汽车从![]() 地匀速行驶到
地匀速行驶到![]() 地,速度不超过
地,速度不超过![]() 千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度
千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米小时)的函效:并求出当
(千米小时)的函效:并求出当![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,此时汽车的速度应调整为多大,才会使得运输成本最小,
,此时汽车的速度应调整为多大,才会使得运输成本最小,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com