
分析 首先进行复数的化简,然后根据要求解答.
解答 解:由已知复数z=$\frac{(1-i)^{2}+3(1+i)}{2-i}$=$\frac{-2i+3+3i}{2-i}$=$\frac{3+i}{2-i}$=$\frac{(3+i)(2+i)}{(2-i)(2+i)}$=$\frac{5+5i}{5}$=1+i;
所以(1)若复数z1与z在复平面上所对应的点关于虚轴对称,则它们实部互为相反数,虚部相等,所以z1=-1+i;
(2)若复数z2=a+bi(a,b∈R)满足z2+ax+b=1-i,
所以(1+i)2+a(1+i)+b=1-i,
整理得a+b+(2+a)i=1-i,
所以a+b=1并且2+a=-1,
解得a=-3,b=4,
所以复数z2=-3+4i,所以z2的共轭复数-3-4i.
点评 本题考查了复数的混合运算以及复数的几何意义、共轭复数;关键是正确化简复数z.


科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | 0或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{x}$ | B. | $\frac{1}{x}$ | C. | -$\frac{1}{{x}^{2}}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
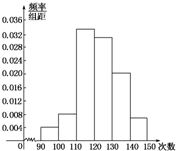 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com