
分析 (1)利用奇函数的定义,即可证明a2+b2=0.
(2)分类讨论:①当x=0时a取任意实数不等式恒成立;②当0<x≤1时f(x)<0恒成立,再转化为x+$\frac{b}{x}$<a<x-$\frac{b}{x}$恒成立问题,利用函数g(x)=x+$\frac{b}{x}$的最值即可求得实数a的取值范围.
解答 解:(1)若f(x)为奇函数
则对任意的x∈R都有f(-x)+f(x)=0恒成立,
即-x|-x-a|+b+x|x-a|+b=0
令x=0,得b=0;令x=a,得a=0.∴a2+b2=0(6分)
(2)由b<2$\sqrt{2}$-3<0,当x=0时a取任意实数不等式恒成立
当0<x≤1时f(x)<0恒成立,也即x+$\frac{b}{x}$<a<x-$\frac{b}{x}$恒成立
令g(x)=x+$\frac{b}{x}$在0<x≤1上单调递增,∴a>gmax(x)=g(1)=1+b(10分)
令h(x)=x-$\frac{b}{x}$,则h(x)在(0,$\sqrt{-b}$]上单调递减,[$\sqrt{-b}$],+∞)单调递增
1°当b<-1时h(x)=x-$\frac{b}{x}$在0<x≤1上单调递减
∴a<hmin(x)=h(1)=1-b.∴1+b<a<1-b.(12分)
2°当-1≤b<2$\sqrt{2}$-3时,h(x)=x-$\frac{b}{x}$≥2$\sqrt{-b}$],
∴a<hmin(x)=2$\sqrt{-b}$],∴1+b<a<2$\sqrt{-b}$].(14分)
点评 本小题主要考查函数单调性、奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,化归与转化思想.属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 2.5 | 3 | 4 | 4.5 | 5.22 | 5.97 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
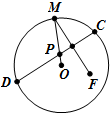 如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )
如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com