
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原,如图所示,平行四边形形状的纸片是由六个边长为![]() 的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球体积的最大值为______.
的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球体积的最大值为______.
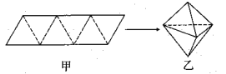
科目:高中数学 来源: 题型:
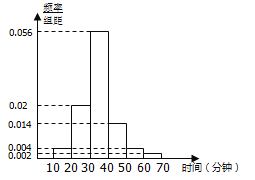
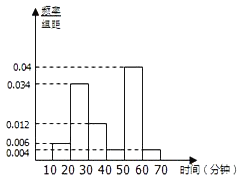
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.
![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,曲线
轴的正半轴重合,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是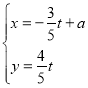 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 是圆
是圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离
的距离![]() 的最小值和最大值;
的最小值和最大值;
(2)直线![]() 与
与![]() 关于原点对称,且直线
关于原点对称,且直线![]() 截曲线
截曲线![]() 的弦长等于
的弦长等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为等腰梯形,四边形
为等腰梯形,四边形![]() 为菱形.已知
为菱形.已知![]() ,
,![]() ,
,![]() .
.
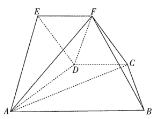
(1)线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(2)若线段![]() 在平面
在平面![]() 上的投影长度为
上的投影长度为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点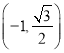 且离心率为
且离心率为![]() .
.
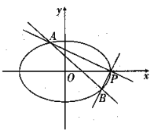
(1)求椭圆![]() 的方程;
的方程;
(2)如图所示,设椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() ,
,![]() 是椭圆上异于点
是椭圆上异于点![]() 的两点,直线
的两点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,试判断直线
,试判断直线![]() 是否经过一个定点?若是,则求出该定点的坐标;若不是,请说明理由.
是否经过一个定点?若是,则求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家正积极推行垃圾分类工作,教育部办公厅等六部门也发布了《关于在学校推进生活垃圾分类管理工作的通知》.《通知》指出,到2020年底,各学校生活垃圾分类知识普及率要达到100%某市教育主管部门据此做了“哪些活动最能促进学生进行垃圾分类”的问卷调查(每个受访者只能在问卷的4个活动中选择一个)如图是调查结果的统计图,以下结论正确的是( )
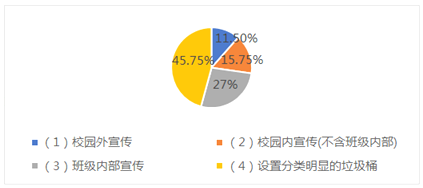
A.回答该问卷的受访者中,选择的(2)和(3)人数总和比选择(4)的人数多
B.回该问卷的受访者中,选择“校园外宣传”的人数不是最少的
C.回答该问卷的受访者中,选择(4)的人数比选择(2)的人数可能多30人
D.回答该问卷的总人数不可能是1000人
查看答案和解析>>
科目:高中数学 来源: 题型:
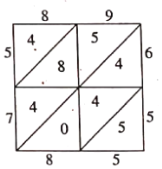
【题目】写算,是一种格子乘法,也是笔算乘法的一种,用以区别筹算与珠算,它由明代数学家吴敬在其撰写的《九章算法比类大全》一书中提出,是从天元式的乘法演变而来.例如计算![]() ,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出
,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出![]() 的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com