练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某大学餐饮中心为了了解新生的饮食习惯，在全校一年级学生中进行了抽样调查，调查结果如下表所示：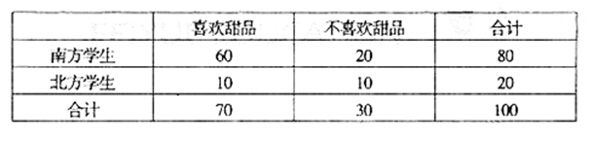

    （1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
    （2）已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率.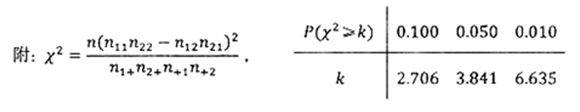

    （1）有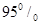的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”； （2）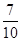

    解析试题分析：（1）将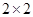列联表中的数据代入公式计算，得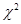的值，然后与表格中的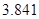比较，若小于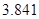，则有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”； （2）从5名学生中随机抽取3人，有10种结果，构成基本事件空间，其中“至多有1人喜欢甜品”这个事件包含7个基本事件，代入古典概型的概率计算公式即可．
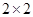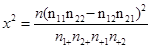
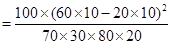
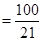
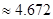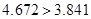    （1）将列联表中的数据代入公式计算．得．由于．所以有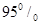
    的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”．
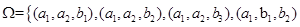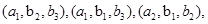
    （2）从5名数学系的学生任取3人的一切可能结果所组成的基本事件空间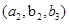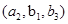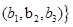， ，，．其中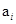表示喜欢甜品的学生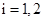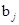，．表示不喜欢甜品的学生，．
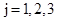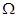    由10个基本事件组成，切这些基本事件出现是等可能的．用A表示“3人中至多有1人喜欢甜品”这一事件，则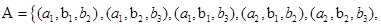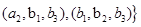．事件A是由7个基本事件组成．因而．
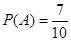    考点：1、独立性检验；2、古典概型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
    （1）若成绩大于等于14秒且小于16秒规定为良好，求该班在这次百米测试中成绩为良好的人数．
    （2）请根据频率分布直方图，估计样本数据的众数和中位数（精确到0.01）．
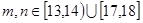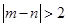    (3)设表示该班两个学生的百米测试成绩，已知，求事件的概率.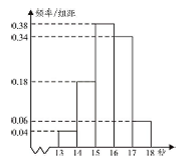

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查，
    统计数据如下表所示：

     
    		积极参加班级工作
    		 不太积极参加班级工作
    		合计
    学习积极性高
    		      18
    		       7
    		 25
    学习积极性一般
    		       6
    		       19
    		 25
    合计
    		      24
    		       26
    		 50
     
    试运用独立性检验的思想方法分析：学生的学习积极性与对待班级的态度是否有关系？

    2

     
    说明理由。

    附：K2=
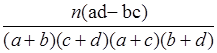
    P(K2≥k0 )
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001
       k0
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某电视台在一次对文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关数据如下表所示：

       
    		文艺节目
    		新闻节目
    		总计
    20岁到40岁
    		40
    		20
    		60
    40岁以上
    		15
    		25
    		40
    总计
    		55
    		45
    		100
     
    （1）用分层抽样方法在收看新闻节目的观众中，随机抽取9名，那么40岁以上的观众应抽取几名？
    （2）由表中数据分析，我们能否有99%的把握认为收看新闻节目的观众与年龄有关？（最后结果保留3位有效数字，四舍五入）
    附：

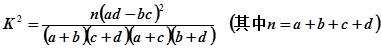
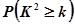    		0.05
    		0.01
    		0.005
    		0.001

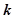    		3.841
    		6.635
    		7.879
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：


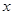    		2
    		3
    		4
    		5
    		6

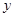    		2.2
    		3.8
    		5.5
    		6.5
    		7.0
     
    已知，，
    (1)在下面坐标系中画出散点图；

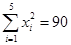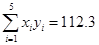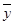    (2)计算，，并求出线性回归方程；
    (3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容，成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示，其中“数学与逻辑”科目的成绩等级为B的考生有10人  
    （1）求该班考生中“阅读与表达”科目中成绩等级为A的人数；
    （2）若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分，该考场共10人得分大于7分，其中2人10分，2人9分，6人8分，从这10人中随机抽取2人，求2人成绩之和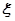的分布列。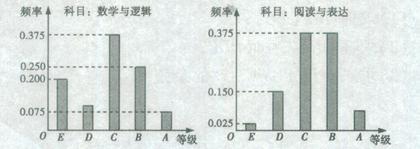

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    近年来，我国很多城市都出现了严重的雾霾天气．为了更好地保护环境，2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:

    组别
    		 PM2.5浓度（微克/立方米）
    		频数（天）
    第一组
    		（0,35]
    		24
    第二组
    		(35,75]
    		48
    第三组
    		(75,115]
    		12
    第四组
    		>115
    		6
     
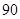    （1）在这天中抽取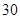天的数据做进一步分析,每一组应抽取多少天?
    （2）在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某种产品的广告费支出z与销售额y（单位：万元）之间有如下对应数据：

    若广告费支出z与销售额y回归直线方程为多一6．5z+n（n∈R）．
    （1）试预测当广告费支出为12万元时，销售额是多少?
    （2）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    以下茎叶图记录了甲，乙两组各三名同学在期末考试中的数学成绩(满分为100分).乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以a表示.

    （1）若甲，乙两个小组的数学平均成绩相同，求a的值.
    （2）求乙组平均成绩超过甲组平均成绩的概率.
    （3）当a=2时，分别从甲，乙两组同学中各随机选取一名同学，求这两名同学的数学成绩之差的绝对值为2分的概率.

    查看答案和解析>>

    同步练习册答案