练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】△ABC的内角A，B，C所对的边分别为a，b，c．向量 =（a， b）与 =（cosA，sinB）平行．
    （Ⅰ）求A；
    （Ⅱ）若a= ，b=2，求△ABC的面积．

    【答案】解：（Ⅰ）因为向量 =（a， b）与 =（cosA，sinB）平行，所以asinB﹣ =0，由正弦定理可知：sinAsinB﹣ sinBcosA=0，因为sinB≠0，
    所以tanA= ，可得A= ；
    （Ⅱ）a= ，b=2，由余弦定理可得：a2=b2+c2﹣2bccosA，可得7=4+c2﹣2c，解得c=3，
    △ABC的面积为： =
    【解析】（Ⅰ）利用向量的平行，列出方程，通过正弦定理求解A；（Ⅱ）利用A，以及a= ，b=2，通过余弦定理求出c，然后求解△ABC的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是（﹣∞，0）∪（0，+∞）上的奇函数，且当x＜0时，函数的部分图象如图所示，则不等式xf（x）＜0的解集是（ ）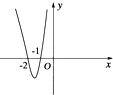

    A.（﹣2，﹣1）∪（1，2）
    B.（﹣2，﹣1）∪（0，1）∪（2，+∞）
    C.（﹣∞，﹣2）∪（﹣1，0）∪（1，2）
    D.（﹣∞，﹣2）∪（﹣1，0）∪（0，1）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

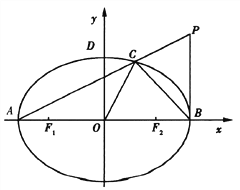
    【题目】已知椭圆的左、右焦点分别为，左、右顶点分别为为直径的圆O过椭圆E的上顶点D，直线DB与圆O相交得到的弦长为．设点，连接PA交椭圆于点C．

    (I)求椭圆E的方程；

    (II)若三角形ABC的面积不大于四边形OBPC的面积，求t的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题：
    ①“等边三角形的三个内角均为60°”的逆命题；
    ②“若k＞0，则方程x2+2x﹣k=0有实根”的逆否命题；
    ③“全等三角形的面积相等”的否命题；
    ④“若 = ，则 ⊥ ”的否命题，
    其中真命题的个数是（ ）
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

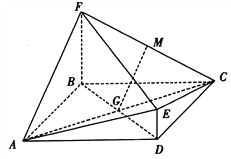
    【题目】如图，菱与四边形BDEF相交于BD， 平面ABCD，DE//BF,BF=2DE，AF⊥FC，M为CF的中点， ．

    (I)求证：GM／／平面CDE；

    (II)求证：平面ACE⊥平面ACF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

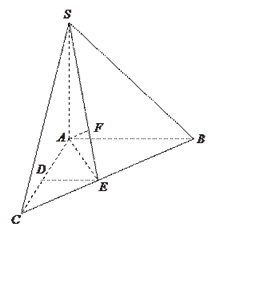
    【题目】如图，在三棱锥中， 底面， ， ， ， 分别是， 的中点， 在上，且．

    （1）求证： 平面；

    （2）在线段上上是否存在点，使二面角

    的大小为？若存在，求出的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ．
    （1）求函数f（x）的定义域和值域；
    （2）判断函数f（x）的奇偶性，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}首项a1=1，公差为d，且数列 是公比为4的等比数列，
    （1）求d；
    （2）求数列{an}的通项公式an及前n项和Sn；
    （3）求数列 的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，分别是棱的中点.

    （1）求证：平面；

    （2）求证：平面平面.

    查看答案和解析>>

    同步练习册答案