解:(1)依题意,n>3时,
S
n=

a
n+1,S
n-1=

a
n-1+1,
两式相减得:
S
n-S
n-1=

a
n-

a
n-1…(1分),
∴a
n=

a
n-

a
n-1?

…(2分)
所以

=
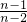
×
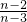
a
n-2=
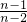
×
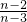
×…×

a
3=

(3分)
n=3时,S
3=

a
3+1,a
1+a
2+a
3=

a
3+1,
解得a
3=4…(4分)
所以n>3时,a
n=2(n-1)…(5分),
而且2(3-1)=4=a
3,2(2-1)=2=a
2,2(1-1)=0≠a
1…(6分),
所以a
n=

…(7分)
(2)依题意,(S
1-34)a
1=-33,(S
2-34)a
2=-62
n>2时,(Sn-34)a
n=2n
3-4n
2-64n+66…(8分),
作函数f(x)=2x
3-4x
2-64x+66,x>2…(9分)
f′(x)=6x
2-8x-64=2(3x+8)(x-4)…(10分),
解得x=4…(11分)
当2<x<4时,f′(x)<0;当x>4时,f′(x)>0…(12分).
所以,f(x)在x=4取得最小值f(4)=-126…(13分),
因为f(4)<-33且f(4)<-62,
所以,数列{(Sn-34)a
n}(n∈N
+)最小的项是(S
4-34)a
4=-126…(14分).
分析:(1)依题意,n>3时,S
n=

a
n+1,S
n-1=

a
n-1+1,两式相减得:S
n-S
n-1=

a
n-

a
n-1从而得出数列a
n的递推式,再利用累乘的方法即可求出数列的通项公式;
(2)依题意先得出(Sn-34)a
n=2n
3-4n
2-64n+66,作函数f(x)=2x
3-4x
2-64x+66,x>2,利用导数研究其单调性得到f(x)在x=4取得最小值,从而得出数列{(Sn-34)a
n}(n∈N
+)最小的项.
点评:本小题主要考查函数单调性的应用、数列递推式、数列的函数特性等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

 an+1.
an+1. an+1,Sn-1=
an+1,Sn-1= an-1+1,
an-1+1, an-
an- an-1…(1分),
an-1…(1分), an-
an- an-1?
an-1? …(2分)
…(2分) =
=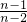 ×
×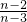 an-2=
an-2=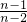 ×
×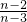 ×…×
×…× a3=
a3= (3分)
(3分) a3+1,a1+a2+a3=
a3+1,a1+a2+a3= a3+1,
a3+1, …(7分)
…(7分) an+1,Sn-1=
an+1,Sn-1= an-1+1,两式相减得:Sn-Sn-1=
an-1+1,两式相减得:Sn-Sn-1= an-
an- an-1从而得出数列an的递推式,再利用累乘的方法即可求出数列的通项公式;
an-1从而得出数列an的递推式,再利用累乘的方法即可求出数列的通项公式;

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案