
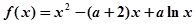 ,其中常数
,其中常数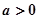 。
。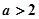 时,求函数
时,求函数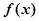 的单调递增区间;
的单调递增区间;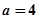 时,是否存在实数
时,是否存在实数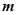 ,使得直线
,使得直线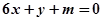 恰为曲线
恰为曲线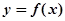 的切线?若存在,求出
的切线?若存在,求出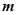 的值;若不存在,说明理由;
的值;若不存在,说明理由;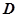 上的函数
上的函数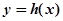 的图象在点
的图象在点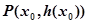 处的切线方程为
处的切线方程为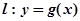 ,当
,当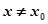 时,若
时,若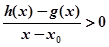 在
在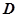 内恒成立,则称
内恒成立,则称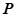 为函数
为函数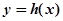 的“类对称点”。当
的“类对称点”。当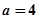 ,试问
,试问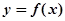 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.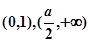 。(2)不存在;(3)
。(2)不存在;(3)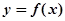 存在“类对称点”,
存在“类对称点”,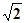 是一个“类对称点”的横坐标。
是一个“类对称点”的横坐标。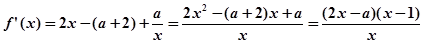 ,其中
,其中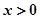 ,…………………. ………. ……………2
,…………………. ………. ……………2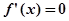 得
得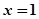 或
或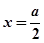 .
.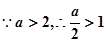 ……………………………
……………………………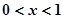 及
及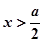 时,
时,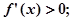 当
当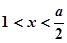 时,
时,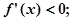 ……………3
……………3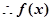 的单调递增区间为
的单调递增区间为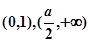 。……………………….4
。……………………….4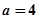 时,
时,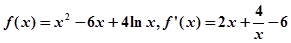 ,其中
,其中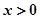 ,
,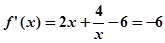 ,…………………………5
,…………………………5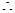 不存在实数
不存在实数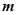 使得直线
使得直线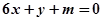 恰为曲线
恰为曲线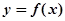 的切线。………7
的切线。………7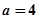 时,函数
时,函数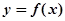 在其图象上一点
在其图象上一点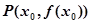 处的切线方程为
处的切线方程为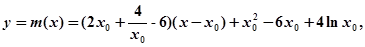 ………………..8
………………..8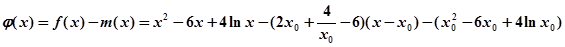 则
则 …………………………………….9
…………………………………….9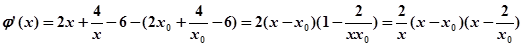
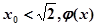 在
在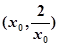 上单调递减,
上单调递减,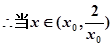 时,
时,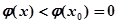 ,此时
,此时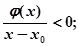 ………………………………….
………………………………….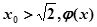 在
在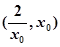 上单调递减,
上单调递减, 时,
时,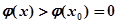 ,此时
,此时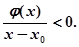 ……………………………………
……………………………………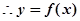 在
在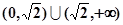 上不存在“类对称点”………………..11
上不存在“类对称点”………………..11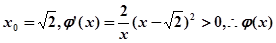 在
在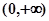 上是增函数,
上是增函数, 时,
时,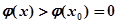 ,当
,当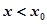 时,
时,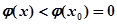 ,故
,故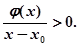
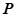 是
是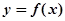 的“类对称点”
的“类对称点”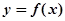 存在“类对称点”,
存在“类对称点”,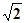 是一个“类对称点”的横坐标。…….14
是一个“类对称点”的横坐标。…….14

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com