
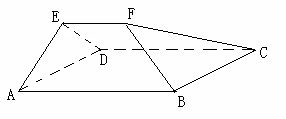
如图:在多面体EF-ABCD中,四边形ABCD是平行四边形,△EAD为正三角形,且平面EAD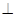 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,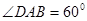 .
.
(Ⅰ)求多面体EF-ABCD的体积;
(Ⅱ)求直线BD与平面BCF所成角的大小.
(1)5(2)
解析试题分析:解(Ⅰ)如图.取AD的中点G,正△EAD中,  ,又AD=2,故
,又AD=2,故  ,又因为平面EAD
,又因为平面EAD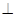 平面ABCD,所以
平面ABCD,所以 ,多面体EF-ABCD的体积
,多面体EF-ABCD的体积 ,而四边形ABCD的面积
,而四边形ABCD的面积 ,所以
,所以 ;设AB的中点为H,因为AB=2EF,所以FH∥AE,所以
;设AB的中点为H,因为AB=2EF,所以FH∥AE,所以 ,所以
,所以 ,所以
,所以 ,故所求多面体EF-ABCD的体积是5
,故所求多面体EF-ABCD的体积是5
(Ⅱ)连接EH,由题设知EF=HB,又EF∥AB,所以四边形EHBF是平行四边形,连接GH,在△AGH中,AH=2AG=2, .故
.故 ,即
,即 ,又
,又 ,所以
,所以 平面EGH,
平面EGH, ,又因为BF∥EH,所以AD
,又因为BF∥EH,所以AD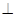 BF,在平行四边形ABCD中,BC∥AD,所以BC⊥BF;又GH⊥AD, GH∥ BD,所以BD ⊥AD,而BC∥AD,故BC⊥BD,所以BC⊥平面DFB,BC
BF,在平行四边形ABCD中,BC∥AD,所以BC⊥BF;又GH⊥AD, GH∥ BD,所以BD ⊥AD,而BC∥AD,故BC⊥BD,所以BC⊥平面DFB,BC 平面BCF,所以平面BCF⊥平面DFB,所以点D在平面BCF上的射影P点在BF上,所以∠FBD就是直线BD与平面BCF所成的角,在△BFD中, BF=HE=
平面BCF,所以平面BCF⊥平面DFB,所以点D在平面BCF上的射影P点在BF上,所以∠FBD就是直线BD与平面BCF所成的角,在△BFD中, BF=HE= ,又BC⊥平面DFB,所以,平面FBD⊥面ABCD,故F点在平面ABCD上的射影K在BD上,且FK=EG=
,又BC⊥平面DFB,所以,平面FBD⊥面ABCD,故F点在平面ABCD上的射影K在BD上,且FK=EG= ,所以
,所以 ,故求直线BD与平面BCF所成角是
,故求直线BD与平面BCF所成角是 。
。
(第(Ⅱ)小题也可用向量解答,略)
考点:几何体体积的求解,以及线面角的求解
点评:解决的关键是利用空间中的几何体的分割法来得到不规则几何体的体积的求解,对于角的求解可以运用几何法也可以运用向量法来得到。属于基础题。


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,直角梯形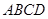 与等腰直角三角形
与等腰直角三角形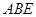 所在的平面互相垂直.
所在的平面互相垂直.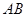 ∥
∥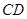 ,
,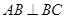 ,
, ,
, .
.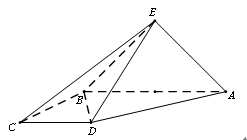
(1)求直线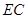 与平面
与平面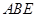 所成角的正弦值;
所成角的正弦值;
(2)线段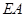 上是否存在点
上是否存在点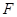 ,使
,使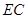 // 平面
// 平面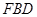 ?若存在,求出
?若存在,求出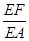 ;若不存在,说明理由.1
;若不存在,说明理由.1
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四边形 中,对角线
中,对角线 于
于 ,
, ,
,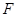 为
为 的重心,过点
的重心,过点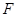 的直线
的直线 分别交
分别交 于
于 且
且 ‖
‖ ,沿
,沿 将
将 折起,沿
折起,沿 将
将 折起,
折起, 正好重合于
正好重合于 .
. 
(Ⅰ) 求证:平面 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 夹角的大小.
夹角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方形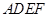 与梯形
与梯形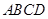 所在的平面互相垂直,
所在的平面互相垂直,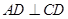 ,
, ∥
∥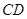 ,
,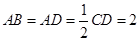 ,点
,点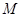 在线段
在线段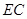 上.
上.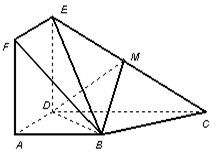
(I)当点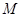 为
为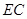 中点时,求证:
中点时,求证: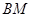 ∥平面
∥平面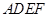 ;
;
(II)当平面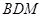 与平面
与平面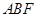 所成锐二面角的余弦值为
所成锐二面角的余弦值为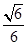 时,求三棱锥
时,求三棱锥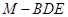 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知△BCD中,∠BCD=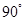 ,BC=CD=1,AB⊥平面BCD,∠ADB=
,BC=CD=1,AB⊥平面BCD,∠ADB=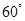 ,E、F分别是AC、AD上的动点,且
,E、F分别是AC、AD上的动点,且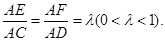
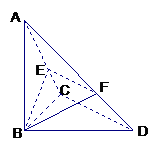
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com