
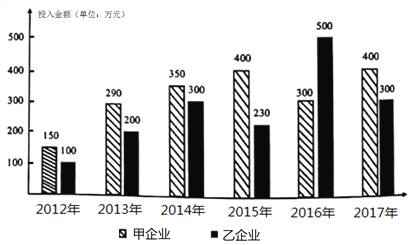
【题目】2018年的政府工作报告强调,要树立绿水青山就是金山银山理念,以前所未有的决心和力度加强生态环境保护.某地科技园积极检查督导园区内企业的环保落实情况,并计划采取激励措施引导企业主动落实环保措施,下图给出的是甲、乙两企业2012年至2017年在环保方面投入金额(单位:万元)的柱状图.
(Ⅰ)分别求出甲、乙两企业这六年在环保方面投入金额的平均数;(结果保留整数)
(Ⅱ)园区管委会为尽快落实环保措施,计划对企业进行一定的奖励,提出了如下方案:若企业一年的环保投入金额不超过200万元,则该年不奖励;若企业一年的环保投入金额超过200万元,不超过300万元,则该年奖励20万元;若企业一年的环保投入金额超过300万元,则该年奖励50万元.
(ⅰ)分别求出甲、乙两企业这六年获得的奖励之和;
(ⅱ)现从甲企业这六年中任取两年对其环保情况作进一步调查,求这两年获得的奖励之和不低于70万元的概率.
【答案】(1)见解析;(2) (ⅰ)190万元,110万元; (ⅱ)![]() .
.
【解析】(Ⅰ)由柱状图可知,甲企业这六年在环保方面的投入金额分别为![]() ,
,
其平均数为![]() (万元);
(万元);
乙企业这六年在环保方面的投入金额分别为![]() ,
,
其平均数为![]() (万元).
(万元).
(Ⅱ)(ⅰ)根据题意可知,企业每年所获得的环保奖励![]() (单位:万元)是关于该年环保投入
(单位:万元)是关于该年环保投入![]() (单位:万元)的分段函数,即
(单位:万元)的分段函数,即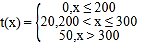 ;
;
所以甲企业这六年获得的奖励之和为:![]() (万元);
(万元);
乙企业这六年获得的奖励之和为:![]() (万元).
(万元).
(ⅱ)由(ⅰ)知甲企业这六年获得的奖金数如下表:
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
奖励(单位:万元) | 0 | 20 | 50 | 50 | 20 | 50 |
奖励共分三个等级,其中奖励0万元的只有2012年,记为![]() ;
;
奖励20万元的有2013年,2016年,记为![]() ;
;
奖励50万元的有2014年,2015年和2017年,记为![]() .
.
故从这六年中任意选取两年,所有的情况为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种.
,共15种.
其中奖励之和不低于70万元的取法为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共9种.
,共9种.
故所求事件的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点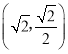 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() ,点
,点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交椭圆
的直线交椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
①若直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
②设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在定点
,是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
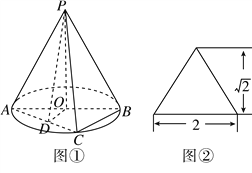
【题目】圆锥![]() 如图①所示,图②是它的正(主)视图.已知圆
如图①所示,图②是它的正(主)视图.已知圆![]() 的直径为
的直径为![]() ,
, ![]() 是圆周上异于
是圆周上异于![]() 的一点,
的一点, ![]() 为
为![]() 的中点.
的中点.
(I)求该圆锥的侧面积S;
(II)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱锥![]() 中,求点
中,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为![]() ,点
,点![]() 在椭圆C上,直线
在椭圆C上,直线![]() 与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 在x轴上是否存在点P,使得无论非零实数k怎样变化,总有
在x轴上是否存在点P,使得无论非零实数k怎样变化,总有![]() 为直角?若存在,求出点P的坐标,若不存在,请说明理由.
为直角?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”.广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极鱼”.已知![]() 或
或 ,下列命题中:①
,下列命题中:①![]() 在平面直角坐标系中表示的区域的面积为
在平面直角坐标系中表示的区域的面积为![]() ;②
;②![]() ,使得
,使得![]() ;③
;③![]() ,都有
,都有![]() 成立;④设点
成立;④设点![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .其中真命题的个数为( )
.其中真命题的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 与
与![]() :
:![]() 相切于点
相切于点![]() .过点
.过点![]() 作两条斜率之积为-2的直线分别交圆
作两条斜率之积为-2的直线分别交圆![]() 于
于![]() ,
,![]() 与
与![]() ,
,![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρ(1-cos2θ)=8cosθ,直线ρcosθ=1与曲线C相交于M,N两点,直线l过定点P(2,0)且倾斜角为α,l交曲线C于A,B两点.
(1)把曲线C化成直角坐标方程,并求|MN|的值;
(2)若|PA|,|MN|,|PB|成等比数列,求直线l的倾斜角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的一个动点,当直线
轴上方的一个动点,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的另外一个交点为
的另外一个交点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com