
 �ҹ�����WTOʱ�����ݴ�ɵ�Э�飬��������ij��Ʒ�Ĺ�˰˰��t���г��۸�x����λ��Ԫ�����г���Ӧ��P֮�������ϵʽ��P=2${\;}^{��l-kt����x-b��^{2}}$������b��kΪ����������t=0.75ʱ��P����x�ĺ�����ͼ����ͼ��ʾ��
�ҹ�����WTOʱ�����ݴ�ɵ�Э�飬��������ij��Ʒ�Ĺ�˰˰��t���г��۸�x����λ��Ԫ�����г���Ӧ��P֮�������ϵʽ��P=2${\;}^{��l-kt����x-b��^{2}}$������b��kΪ����������t=0.75ʱ��P����x�ĺ�����ͼ����ͼ��ʾ������ ��1������ͼ�����k��b��ֵ��
��2����p=qʱ���ɵ�2��1-t����x-5��2=2-x�������t=1+$\frac{1}{x+\frac{25}{x}-10}$����˫������f��x��=x+$\frac{25}{x}$�ڣ�0��4]�ϵ����ݼ�����֪��x=4ʱ��f��x������Сֵ��
��� �⣺��1����ͼ��֪��t=0.75ʱ��$\left\{\begin{array}{l}{{2}^{��1-0.75t����5-b��^{2}=1}}\\{{2}^{��1-0.75t����7-b��^{2}=7}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{b=5}\end{array}\right.$��
��2����P=Qʱ����${2}^{��1-t����x-5��^{2}}$=2-x��
��ã�t=1+$\frac{x}{��x-5��^{2}}$=1+$\frac{1}{x+\frac{25}{x}-10}$��
��f��x��=x+$\frac{25}{x}$�ڣ�0��4]�ϵ����ݼ���
�൱x=4ʱ��f��x������Сֵ$\frac{41}{4}$��
��ʱt=1+$\frac{1}{x+\frac{25}{x}-10}$��
ȡ�����ֵ5��
�ʵ�x=4ʱ����˰˰�ʵ����ֵΪ500%��
���� ������Ҫ���麯��ģ�͵�Ӧ�ã�������ָ�����̵Ľⷨ��˫��������ֵ����


 ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д� ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}��$ | B�� | $\frac{1}{3}��$ | C�� | $\frac{1}{2}��$ | D�� | $\frac{5}{6}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��$\frac{k��}{2}$+$\frac{3��}{8}$��k��Z} | B�� | {x|x��$\frac{k��}{2}$+$\frac{3��}{4}$��k��Z} | C�� | {x|x��k��+$\frac{3��}{8}$��k��Z} | D�� | {x|x��k��+$\frac{3��}{4}$��k��Z} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
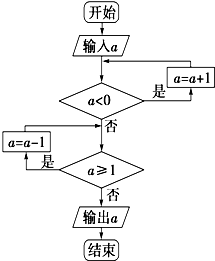 ����������ͼ��ʾ�ij����ͼ������һ����ڶ��������a��ֵ֮��Ϊ0�����һ����ڶ��������a��ֵ֮��Ϊ��������
����������ͼ��ʾ�ij����ͼ������һ����ڶ��������a��ֵ֮��Ϊ0�����һ����ڶ��������a��ֵ֮��Ϊ��������| A�� | 0 | B�� | 1 | C�� | 0��1 | D�� | -1��1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com