练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．由点（2，2）向圆（x-3）2+y2=1引切线，则切线段长为2．

    分析 算出圆心为A（3，0）、半径r=1，根据两点间的距离公式，算出点P（2，2）到圆心的距离为|AP|=$\sqrt{1+4}$=$\sqrt{5}$，再由切线的性质利用勾股定理加以计算，可得经过点P的切线长．

    解答 解：∵（x-3）2+y2=1的圆心为A（3，0）、半径r=1，
    ∴点P（2，2）到圆心的距离为|AP|=$\sqrt{1+4}$=$\sqrt{5}$．
    ∵过切点的半径与切线垂直，
    ∴根据勾股定理，得切线长为$\sqrt{5-1}$=2．
    故答案为：2．

    点评 本题已知点P为圆外一个定点，求圆的经过点P的切线长．着重考查了圆的标准方程、两点间的距离公式、切线的性质与勾股定理等知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．函数f（x）=$\frac{{e}^{x}+m}{{e}^{x}+1}$，（m为常数），若对于任意实数a，b，c，总有f（a）+f（b）＞f（c）恒成立，则实数m的取值范围为[$\frac{1}{2}$，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知f（x）为二次函数，f（0）=2，且满足f（x+1）-f（x）=2x-1．
    （1）求f（x）的表达式；
    （2）当x∈[-2，2]时，求函数的值域；
    （3）当∈[t，t+1]时，求f（x）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．正三角形的一个顶点位于原点，另外两个顶点在抛物线y2=x上，则它的边长为2$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

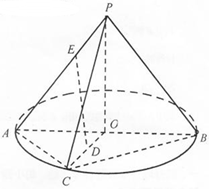    8．如图，圆锥的轴截面PAB是等腰直角三角形，AB的中点为O，C是底面圆周上异于A，B的任意一点，D为线段OC的中点，E为母线PA上一点，且AE=3EP．
    （1）证明：ED∥平面PCB；
    （2）若二面角A-OP-C的大小为90°，求二面角A-PC-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知y=asinx+bcosx+c的图象有一个最低点（$\frac{11π}{6}$，1），如果图象各点纵坐标不变，横坐标缩短为原来的$\frac{3}{π}$倍，再向左平移1个单位，可得到y=f（x）的图象．又直线y=3与y=f（x）每相邻两个交点的距离均为3．
    （1）求y=f（x）的解析式；
    （2）若y=f（x）在[$\frac{π}{6}$，l]上单调，求l的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知A（x1，y1）是抛物线y2=4x上的一个动点，B（x2，y2）是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的一个动点，定点N（1，0），若AB∥x轴，且x1＜x2，则△NAB的周长l的取值范围是（　　）
    A．（$\frac{2}{3}$，2）B．（$\frac{10}{3}$，4）C．（$\frac{51}{16}$，4）D．（2，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．我国加入WTO时，根据达成的协议，若干年内某产品的关税税率t、市场价格x（单位：元）与市场供应量P之间满足关系式：P=2${\;}^{（l-kt）（x-b）^{2}}$，其中b，k为正常数，当t=0.75时，P关于x的函数的图象如图所示：
    （1）试求b，k的值；
    （2）记市场需求量为Q，它近似满足Q（x）=2-x，当时P=Q，市场价格称为市场平衡价格，当市场平衡价格不超过4元时，求税率的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，以Ox轴的非负半轴为始边作两个锐角α，β，它们的终边分别与单位圆交于A，B两点，已知A，B的纵坐标分别为$\frac{\sqrt{5}}{5}$，$\frac{3\sqrt{10}}{10}$
    （1）求α-β；
    （2）求cos（2α-β）的值．

    查看答案和解析>>

    同步练习册答案