
分析 (1)根据三角函数的定义和平方关系,求出α、β的正弦和余弦值,由α、β的范围求出α-β的范围,由两角差的正弦公式求出sin(α-β),在求出α-β的值;
(2)由(2α-β)=(α-β)+α和两角和的余弦公式,求出cos(2α-β)的值.
解答 解:(1)由题意得,$sinα=\frac{\sqrt{5}}{5}$,$sinβ=\frac{3\sqrt{10}}{10}$…2
∵sin2α+cos2α=1,∴cos2α=1-sin2α=$\frac{20}{25}$,
又α是锐角,则cosα=$\frac{2\sqrt{5}}{5}$,…3
同理可求,cosβ=$\frac{\sqrt{10}}{10}$;…4
∵$0<α<\frac{π}{2}$,$0<β<\frac{π}{2}$,∴$-\frac{π}{2}<α-β<\frac{π}{2}$,…5
且sin(α-β)=sinαcosβ-cosαsinβ
=$\frac{\sqrt{5}}{5}×\frac{\sqrt{10}}{10}-\frac{2\sqrt{5}}{5}×\frac{3\sqrt{10}}{10}$=$-\frac{\sqrt{2}}{2}$…7
∴α-β=-$\frac{π}{4}$;…8
(2)由(1)得cos(α-β)=cos($-\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$…9
∴cos(2α-β)=cos[(α-β)+α]
=cos(α-β)cosα-sin(α-β)sinα
=$\frac{\sqrt{2}}{2}×\frac{2\sqrt{5}}{5}-(-\frac{\sqrt{2}}{2})×\frac{\sqrt{5}}{5}$=$\frac{3\sqrt{10}}{10}$.…12
点评 本题考查了三角函数的定义和平方关系,两角差的正弦公式,以及两角和的余弦公式,注意角的范围,考查角之间的关系,以及化简、计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x≠$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z} | B. | {x|x≠$\frac{kπ}{2}$+$\frac{3π}{4}$,k∈Z} | C. | {x|x≠kπ+$\frac{3π}{8}$,k∈Z} | D. | {x|x≠kπ+$\frac{3π}{4}$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2) | C. | (-$\frac{1}{2}$,2) | D. | ($\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,H在圆上,过点H作圆的切线BC,AB,AC分别交圆于点M,N.
如图,A,H在圆上,过点H作圆的切线BC,AB,AC分别交圆于点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
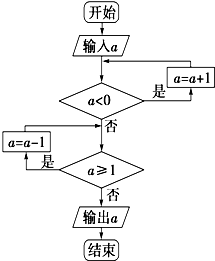 运行两次如图所示的程序框图,若第一次与第二次输入的a的值之和为0,则第一次与第二次输出的a的值之和为( )
运行两次如图所示的程序框图,若第一次与第二次输入的a的值之和为0,则第一次与第二次输出的a的值之和为( )| A. | 0 | B. | 1 | C. | 0或1 | D. | -1或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com