
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2) | C. | (-$\frac{1}{2}$,2) | D. | ($\frac{1}{2}$,2) |
分析 求出原函数的导函数,设出切点坐标,由切点处的导数等于-4求得答案.
解答 解:设切点为P(${x}_{0},\frac{1}{{x}_{0}}$),由y=$\frac{1}{x}$,得y′=-$\frac{1}{{x}^{2}}$,
∴$y′{|}_{x={x}_{0}}=-\frac{1}{{{x}_{0}}^{2}}$,由$-\frac{1}{{{x}_{0}}^{2}}=-4$,解得${x}_{0}=±\frac{1}{2}$.
∴点P的坐标为($\frac{1}{2}$,2)或($-\frac{1}{2}$,-2).
故选:B.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
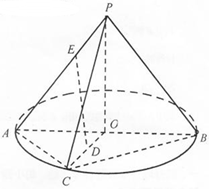 如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.
如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{\sqrt{x}}$ | B. | y=$\frac{lnx}{x}$ | C. | y=xex | D. | y=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 60 | C. | 120 | D. | 135 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com