
分析 (1)首先利用焦点到直线的距离求出c,又$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{10}$,a2=b2+c2,联立解出即可得出.
(2)设直线AB的方程为:x=my+$\frac{6}{\sqrt{5}}$,A(x1,y1),B(x2,y2).联立得到方程组,利用根与系数的关系对|QA|与|QB|进行转化,要注意对特殊情况进行验证.
解答 解:(1)由右焦点(c,0)到直线x-y+3$\sqrt{2}$=0的距离为5,可得:$\frac{|c+3\sqrt{2}|}{\sqrt{2}}$=5,解得c=2$\sqrt{2}$.
又$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{10}$,a2=b2+c2,联立解得a=3,b=1.
∴椭圆C的标准方程为$\frac{{x}^{2}}{9}+{y}^{2}$=1.
(2)当直线与x轴重合时,$\frac{1}{{{{|{QA}|}^2}}}$+$\frac{1}{{{{|{QB}|}^2}}}$=$\frac{1}{(\frac{6\sqrt{5}}{5}+3)^{2}}$+$\frac{1}{(\frac{6\sqrt{5}}{5}-3)^{2}}$=10.
当直线与x轴不重合时,设直线AB的方程为:x=my+$\frac{6}{\sqrt{5}}$,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{x=my+\frac{6}{\sqrt{5}}}\\{{x}^{2}+9{y}^{2}=9}\end{array}\right.$,化为:(m2+9)y2+$\frac{12m}{\sqrt{5}}$y-$\frac{9}{5}$=0,△>0,
∴y1+y2=$-\frac{12m}{\sqrt{5}({m}^{2}+9)}$,y1y2=$\frac{-9}{5({m}^{2}+9)}$.
∴$\frac{1}{|QA{|}^{2}}$=$\frac{1}{({x}_{1}-\frac{6}{\sqrt{5}})^{2}+{y}_{1}^{2}}$=$\frac{1}{({m}^{2}+1){y}_{1}^{2}}$,同理可得:$\frac{1}{|QB{|}^{2}}$=$\frac{1}{({m}^{2}+1){y}_{2}^{2}}$.
∴$\frac{1}{{{{|{QA}|}^2}}}$+$\frac{1}{{{{|{QB}|}^2}}}$=$\frac{1}{({m}^{2}+1){y}_{1}^{2}}$+$\frac{1}{({m}^{2}+1){y}_{2}^{2}}$=$\frac{{y}_{1}^{2}+{y}_{2}^{2}}{({m}^{2}+1){y}_{1}^{2}{y}_{2}^{2}}$=$\frac{({y}_{1}+{y}_{2})^{2}-2{y}_{1}{y}_{2}}{({m}^{2}+1){y}_{1}^{2}{y}_{2}^{2}}$=$\frac{[\frac{-12m}{\sqrt{5}({m}^{2}+9)}]^{2}+\frac{2×9}{5({m}^{2}+9)}}{({m}^{2}+1)[\frac{-9}{5({m}^{2}+9)}]^{2}}$=10.
综上可得:$\frac{1}{{{{|{QA}|}^2}}}$+$\frac{1}{{{{|{QB}|}^2}}}$=10.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、点到直线的距离公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,2)或(-$\frac{1}{2}$,-2) | C. | (-$\frac{1}{2}$,2) | D. | ($\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,H在圆上,过点H作圆的切线BC,AB,AC分别交圆于点M,N.
如图,A,H在圆上,过点H作圆的切线BC,AB,AC分别交圆于点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
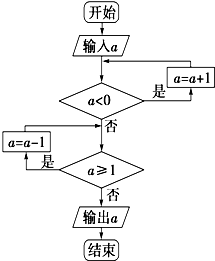 运行两次如图所示的程序框图,若第一次与第二次输入的a的值之和为0,则第一次与第二次输出的a的值之和为( )
运行两次如图所示的程序框图,若第一次与第二次输入的a的值之和为0,则第一次与第二次输出的a的值之和为( )| A. | 0 | B. | 1 | C. | 0或1 | D. | -1或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤1} | B. | {x|-3≤x≤-1} | C. | {x|x<-3或x>-1} | D. | {x|x≤1或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com